Logo

Giải SBT Toán 10 trang 75, 76 tập 1 bài 3 chương 3 đầy đủ nhất

Giải SBT Toán lớp 10 trang 75, 76 tập 1 bài 3 chương 3: Phương trình và hệ phương trình bậc nhất nhiều ẩn đầy đủ hỗ trợ các em học sinh củng cố kiến thức và hiểu rõ phương pháp giải các dạng bài tập trong sách bài tập
4.0
2 lượt đánh giá

Nội dung bài viết

  1. Giải bài 12 SBT Toán 10 tập 1 trang 75
  2. Giải SBT Toán lớp 10 tập 1 bài 13 trang 76
  3. Giải Toán lớp 10 SBT tập 1 bài 14 trang 76
  4. Giải bài 15 trang 76 sách bài tập Toán 10 tập 1
  5. Giải SBT Toán lớp 10 tập 1 bài 16 trang 76
  6. Giải bài 17 sách bài tập Toán 10 tập 1 trang 76
  7. Giải bài 18 trang 76 SBT Toán lớp 10 tập 1 

Giải Toán lớp 10 tập 1 sách bài tập bài 3 chương 3: Phương trình và hệ phương trình bậc nhất nhiều ẩn được giải đáp chi tiết và rõ ràng nhất, giúp cho các bạn học sinh có thể tham khảo và chuẩn bị tốt nhất cho bài học sắp tới nhé.

Giải bài 12 SBT Toán 10 tập 1 trang 75

Giải các hệ phương trình

a) \left\{ \matrix{5x + 3y = - 7 \hfill \cr 2x - 4y = 6 \hfill \cr} \right.

b) \left\{ \matrix{7x + 14y = 17 \hfill \cr 2x + 4y = 5 \hfill \cr} \right.

c) \left\{ \matrix{{2 \over 5}x + {3 \over 7}y = {1 \over 3} \hfill \cr {5 \over 3}x - {5 \over 7}y = {2 \over 3} \hfill \cr} \right.

d) \left\{ \matrix{- 0,2x + 0,5y = 1,7 \hfill \cr 0,3x - 0,4y = 0,9 \hfill \cr} \right.

Lời giải:

a)

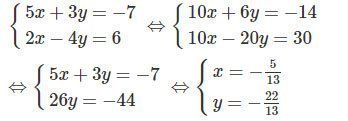
Giải bài tập Toán 10 SBT bài 3 chương 3

b)

\left\{ \matrix{7x + 14y = 17 \hfill \cr 2x + 4y = 5 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{14x + 28y = 34 \hfill \cr 14x + 28y = 35 \hfill \cr} \right. \Rightarrow Hệ phương trình vô nghiệm.

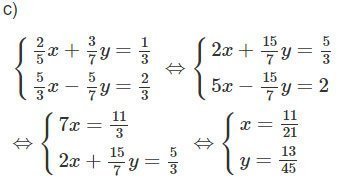
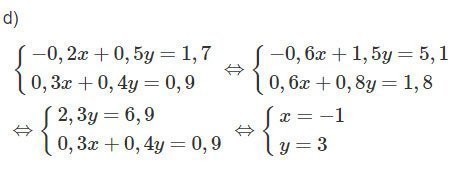
Giải bài tập Toán 10 SBT bài 3 chương 3

Giải bài tập Toán 10 SBT bài 3 chương 3

Giải SBT Toán lớp 10 tập 1 bài 13 trang 76

Một công ti có 85 xe chở khách gồm hai loại, xe chở được 4 khách và xe chở được 7 khách. Dùng tất cả số xe đó, tối đa công ti chở một lần được 445 khách. Hỏi công ti đó có mấy xe mỗi loại?

Lời giải:

Gọi x là số xe 4 chỗ, y là số xe 7 chỗ. Điều kiện x và y nguyên dương.

Ta có hệ phương trình.

\left\{ \matrix{x + y = 85 \hfill \cr 4x + 7y = 445 \hfill \cr} \right. = > \left\{ \matrix{x = 50 \hfill \cr y = 35 \hfill \cr} \right.

(thỏa mãn điều kiện của bài toán).

Vậy công ty có 50 xe 4 chỗ và 35 xe 7 chỗ.

Giải Toán lớp 10 SBT tập 1 bài 14 trang 76

Giải các hệ phương trình

a) \left\{ \matrix{x - 2y + z = 12 \hfill \cr 2x - y + 3z = 18 \hfill \cr - 3x + 3y + 2z = - 9 \hfill \cr} \right.

b) \left\{ \matrix{x + y + z = 7 \hfill \cr 3x - 2y + 2z = 5 \hfill \cr 4x - y + 3z = 10 \hfill \cr} \right.

Lời giải:

a)

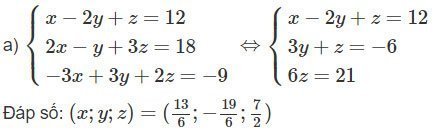
Giải bài tập Toán 10 SBT bài 3 chương 3

b)

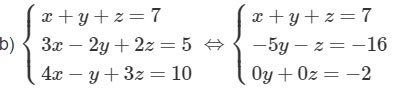
Giải bài tập Toán 10 SBT bài 3 chương 3

Hệ phương trình vô nghiệm.

Giải bài 15 trang 76 sách bài tập Toán 10 tập 1

Giải các hệ phương trình sau bằng máy tính bỏ túi

a) \left\{ \matrix{{3 \over 4}x - {7 \over 3}y = {4 \over 5} \hfill \cr {2 \over 5}x + {2 \over 7}y = {2 \over 9} \hfill \cr} \right.

b) \left\{ \matrix{3,7x + 4,3y = - 2,5 \hfill \cr - 5,1x + 2,7y = 4,8 \hfill \cr} \right.

Lời giải:

Đáp số: a) (x;y) = ({{1412} \over {2169}}; - {{161} \over {1205}});

b) (x;y) \approx ( - 0,86;0,16)

Giải SBT Toán lớp 10 tập 1 bài 16 trang 76

Giải các hệ phương trình sau bằng máy tính bỏ túi

a) \left\{ \matrix{3{x_1} + 4{x_2} - 5{x_3} = 12 \hfill \cr - 4{x_1} + 2{x_2} + 7{x_3} = 7 \hfill \cr 5{x_1} + 6{x_2} - 4{x_3} = 12 \hfill \cr} \right.

b) \left\{ \matrix{0,3x - 4,7y + 2,3z = 4,9 \hfill \cr - 2,1x + 3,2y + 4,5z = 7,6 \hfill \cr 4,2x + 2,7y + 3,7z = 5,7 \hfill \cr} \right.

Lời giải:

Đáp số: a) ({x_1},{x_2},{x_3}) \approx ( - 2,52;3,2; - 1,35);

b) (x;y;z) \approx ( - 0,29; - 0,22;1,71)

Giải bài 17 sách bài tập Toán 10 tập 1 trang 76

Một chủ cửa hàng bán lẻ mang 1 500 000 đồng đến ngân hàng đổi tiền để trả lại cho người mua. Ông ta đổi được tất cả 1 450 đồng tiền xu các loại 2000 đồng, 1000 đồng và 500 đồng. Biết rằng số tiền xu loại 1 000 đồng bằng hai lần hiệu của số tiền xu loại 500 đồng với số tiền xu loại 2000 đồng. Hỏi mỗi loại có bao nhiêu đồng tiền xu?

Lời giải:

Gọi x, y, z lần lượt là số đồng tiền xu loại 2000 đồng, 1000 đồng, 500 đồng.

Điều kiện là x, y, z nguyên dương

Ta có hệ phương trình

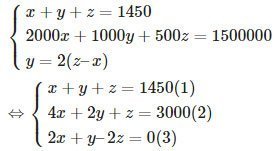
Giải bài tập Toán 10 SBT bài 3 chương 3

Trừ từng vế tương ứng của phương trình (2) với phương trình (1) ta được

3x + y = 1550

Cộng từng vế tương ứng của các phương trình (1), (2) và (3) ta có:

7x + 4y = 4450.

Giải hệ gồm hai phương trình (4) và (5) ta được.

x = 350, y = 500.

Thay các giá trị của x, y vào phương trình (1) ta được z = 600.

Vậy cửa hàng đổi được 350 đồng tiền xu loại 2000 đồng, 500 đồng tiền loại 1000 đồng và 600 đồng tiền xu loại 500 đồng.

Giải bài 18 trang 76 SBT Toán lớp 10 tập 1 

Tìm giá trị của m để các hệ phương trình sau vô nghiệm

a) \left\{ \matrix{3x + 2y = 9 \hfill \cr mx - 2y = 2; \hfill \cr} \right.

b) \left\{ \matrix{2x - my = 5 \hfill \cr x + y = 7. \hfill \cr} \right.

Lời giải:

a) \left\{ \matrix{3x + 2y = 9 \hfill \cr mx - 2y = 2 \hfill \cr} \right. = > (m + 3)x = 11

Phương trình cuối vô nghiệm khi m = -3.

Vậy hệ phương trình đã cho vô nghiệm khi m = -3.

b) \left\{ \matrix{2x - my = 5 \hfill \cr x + y = 7 \hfill \cr} \right. = > \left\{ \matrix{2x - my = 5 \hfill \cr 2x + 2y = 14 \hfill \cr} \right. = > (m + 2)y = 9

Phương trình cuối vô nghiệm khi m = -2.

Vậy với m =- 2 hệ phương trình đã cho vô nghiệm.

CLICK NGAY vào nút TẢI VỀ dưới đây để download Giải sách bài tập Toán lớp 10 tập 1 trang 75, 76 file word, pdf hoàn toàn miễn phí.

Đánh giá bài viết
4.0
2 lượt đánh giá
CÔNG TY CỔ PHẦN TRUYỀN THÔNG HDC VIỆT NAM
Tầng 3, toà nhà S3, Vinhomes Skylake, đường Phạm Hùng, quận Nam Từ Liêm, Hà Nội
Liên hệ quảng cáo: tailieucom123@gmail.com
Copyright © 2020 Tailieu.com
DMCA.com Protection Status