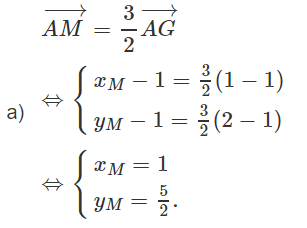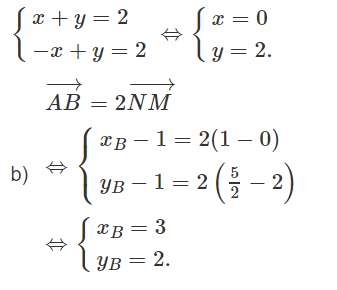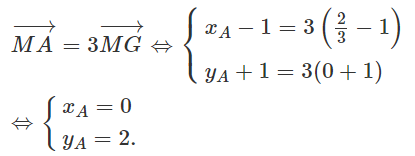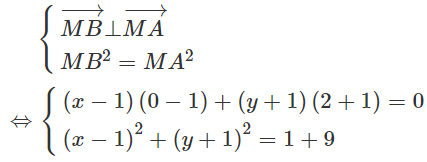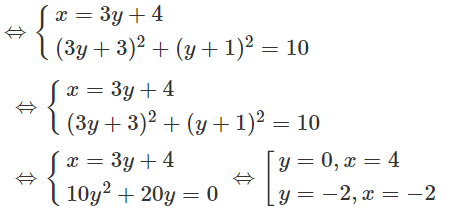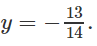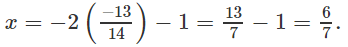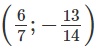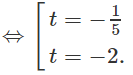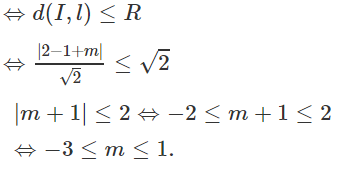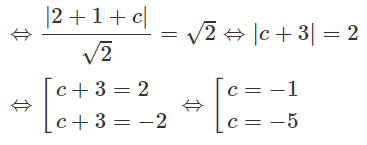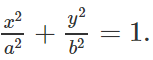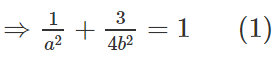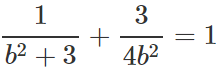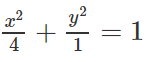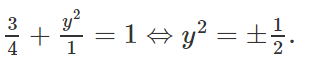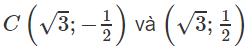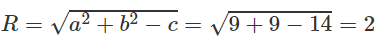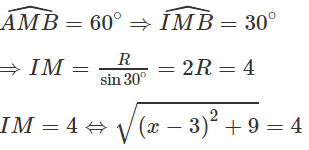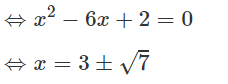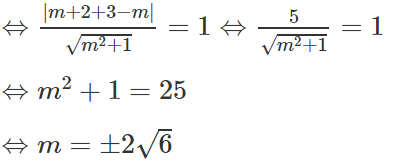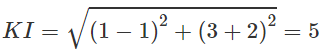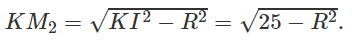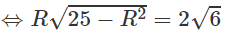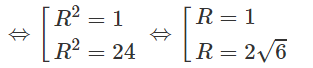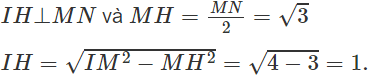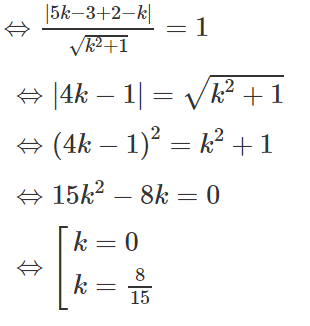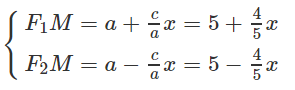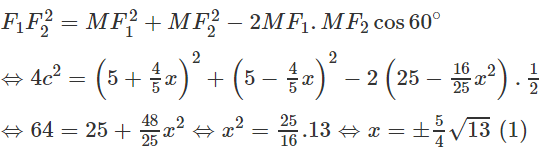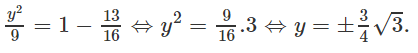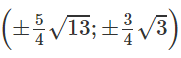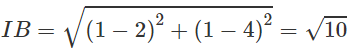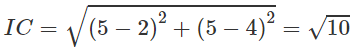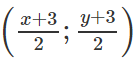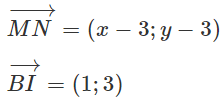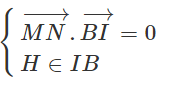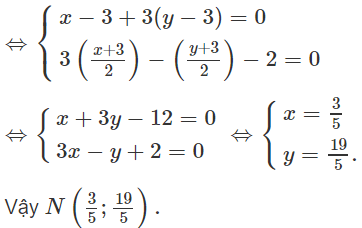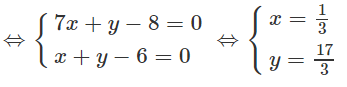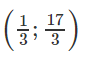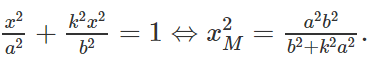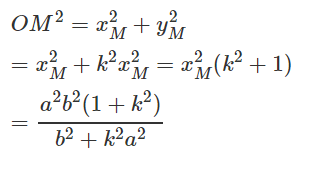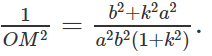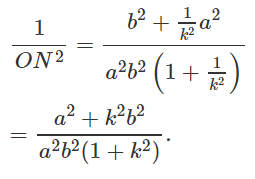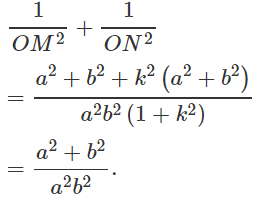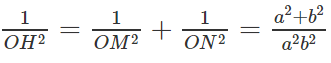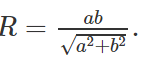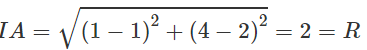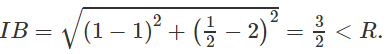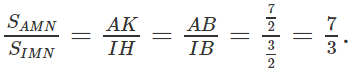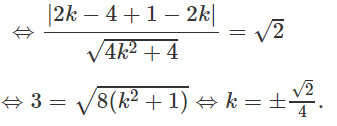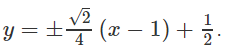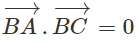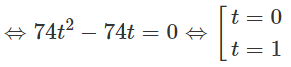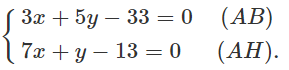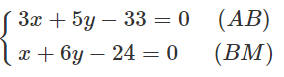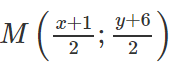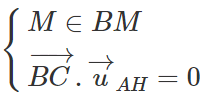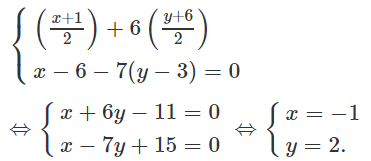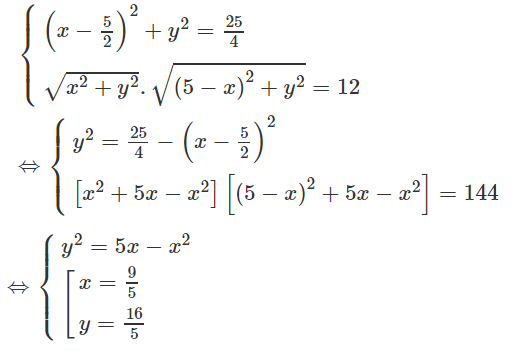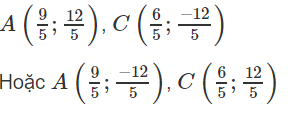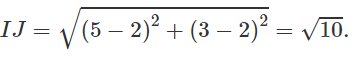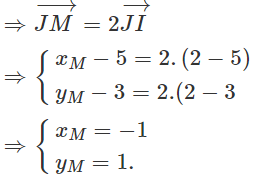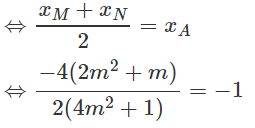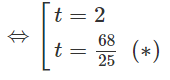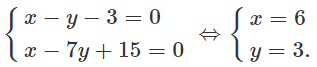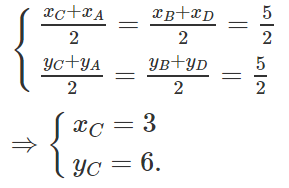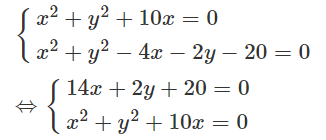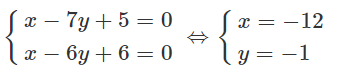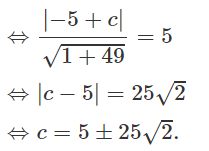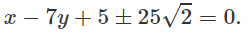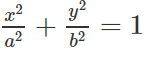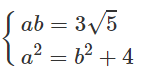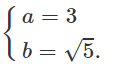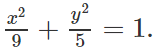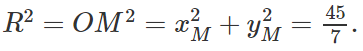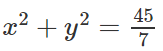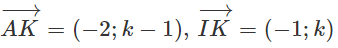Giải SBT Toán hình học 10 trang 201, 202, 203, 204 tập 1: Ôn tập cuối năm

Giải sách bài tập Toán 10 tập 1: Ôn tập cuối năm được giải đáp chi tiết và rõ ràng nhất, giúp cho các bạn học sinh có thể tham khảo và chuẩn bị tốt nhất cho bài học sắp tới nhé.

Giải bài 1 SBT Toán hình 10 tập 1 trang 201

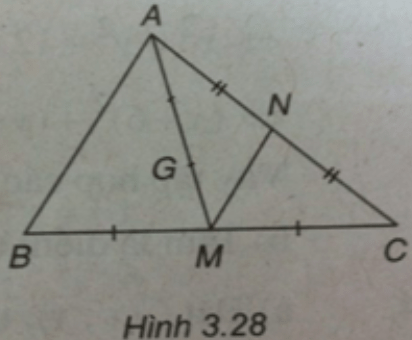
Trong mặt phẳng Oxy cho tam giác ABC, biết đỉnh A(1 ; 1) và tọa độ trọng tâm G(1 ; 2). Cạnh AC và đường trung trực của nó lần lượt có phương trình là x + y - 2 = 0 và - x + y - 2 = 0. Các điểm M và N lần lượt là trung điểm của BC và AC.

    a) Hãy tìm tọa độ các điểm M và N.

    b) Viết phương trình hai đường thẳng chứa hai cạnh AB và BC.

Lời giải:

    (h.3.28)

    Vậy M có tọa độ là (1; 5/2)

    Điểm N(x ; y) thỏa mãn hệ phương trình

    Đường thẳng chứa cạnh AB đi qua hai điểm A(1 ;1) và B(3 ; 2) nên có phương trình : x - 2y + 1=0.

    Đường thẳng chứa cạnh BC đi qua hai điểm B(3 ; 2) và C(1; 5/2) nên có phương trình: x + 4y - 11 = 0

Giải sách bài tập Toán hình 10 tập 1 bài 2 trang 201

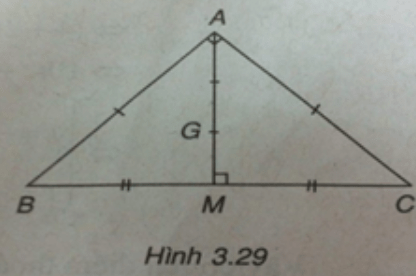
Trong mặt phẳng Oxy cho tam giác ABC có AB = AC, góc BAC = 90^ο. Biết M(1;-1) là trung điểm cạnh BC và G(2/3;0) là trọng tâm tam giác ABC. Tìm tọa độ các đỉnh A, B, C.

Lời giải:

    (h.3.29)

    Vậy A có tọa độ (0;2).

    Đặt B(x;y) ta có :

    Vậy ta có tọa độ của điểm B và C như sau : B(4;0), C(-2;-2) hoặc B(-2;-2), C(4;0).

Giải Toán hình lớp 10 SBT tập 1 bài 3 trang 201

Cho ba điểm A(1;2), B(-3;1), C(4;-2).

    a) Chứng minh rằng tập hợp các điểm M(x;y) thỏa mãn MA² + MB² = MC² là một đường tròn.

    b) Tìm tọa độ tâm và bán kính của đường tròn nói trên.

Lời giải:

    a) MA² + MB² = MC²

    ⇔ (x - 1)² + (y - 2)² + (x + 3)² + (y - 1)² = (x - 4)² + (y + 2)²

    ⇔ x² + y² + 12x - 10y - 5 = 0

    ⇔ (x + 6)² + (y - 5)² = 66

    Vậy tập hợp các điểm M là một đường tròn.

    b) Tâm là điểm (-6 ; 5) bán kính bằng √66

Giải bài 4 trang 201 SBT Toán hình 10 tập 1

Cho hai điểm A(3;-1), B(-1;-2) và đường thẳng d có phương trình x + 2y + 1 = 0

    a) Tìm tọa độ điểm C trên đường thẳng d sao cho tam giác ABC là tam giác cân tại C.

    b) Tìm tọa độ điểm M trên đường thẳng d sao cho tam giác AMB vuông tại M.

Lời giải:

    a) Đặt C(x;y), ta có: C ∈ d ⇔ x = -2y - 1. Vậy C(-2y - 1; y)

    Tam giác ABC cân tại C khi và chỉ khi

    CA = CB ⇔ CA² = CB²

    ⇔ (3 + 2y + 1)² + (-1 - y)² = (-1 + 2y + 1)² + (-2 - y)²

    ⇔ (4 + 2y)² + (1 + y)² = 4y² + (2 + y)²

    Giải ra ta được 

    Vậy C có tọa độ là 

    b) Xét điểm M(-2t - 1;t) trên d, ta có :

    Góc AMB = 90^ο ⇔ AM² + BM² = AB²

    ⇔ (4 + 2t)² + (1 + t)² + 4t² + (2 + t)² = 17

    ⇔ 10t² + 22t + 4 = 0

    Vậy có hai điểm thỏa mãn đề bài là 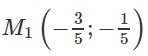 và M₂(3;-2)

Giải SBT Toán hình học lớp 10 tập 1 bài 5 trang 201

Trong mặt phẳng Oxy cho đường tròn (T) có phương trình:

    x² + y² - 4x - 2y + 3 = 0

    a) Tìm tọa độ tâm và tính bán kính của đường tròn (T).

    b) Tìm m để đường thẳng y = x + m có điểm chung với đường tròn (T).

    c) Viết phương trình tiếp tuyến Δ với đường tròn (T) biết rằng Δ vuông góc vơi đường thẳng d có phương trình x - y + 2006 = 0.

Lời giải:

    a) Đường tròn (T) có tâm là điểm (2 ; 1) và có bán kính bằng √2

    b) Đường thẳng l: x - y + m = 0. Ta có:

    l có điểm chung với (T)

    c) Δ ⊥ d nên Δ có phương trình x + y + c = 0.

    Ta có : Δ tiếp xúc với (T) khi và chỉ khi:

    d(I; Δ) = R

    Vậy có hai tiếp tuyến với (T) thỏa mãn đề bài là :

     Δ₁: x + y - 1 = 0

     Δ₂: x + y - 5 = 0

Giải bài 6 sách bài tập Toán hình 10 tập 1 trang 201

Trong mặt phẳng Oxy cho elip (E) có tiêu điểm thứ nhất là (-√3;0) và đi qua điểm 

    a) Hãy xác định tọa độ các đỉnh của (E).

    b) Viết phương trình chính tắc của (E).

    c) Đường thẳng đi qua tiêu điểm thứ hai của elip (E) và vuông góc với trục Ox và cắt (E) tại hai điểm C và D. Tính độ dài đoạn thẳng CD.

Lời giải:

    a) (E) có tiêu điểm F₁(-√3;0) nên c = √3.

    Phương trình chính tắc của (E) có dạng 

    Ta có: 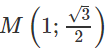 ∈ (E)

    Và a² = b² + c² = b² + 3

    Thay vào (1) ta được :

    ⇔ 4b² + 3b² + 9 = 4b²(b + 3)

    ⇔ 4b⁴ + 5b² - 9 = 0 ⇔ b² = 1

    Suy ra: a² = 4

    Ta có a = 2 ; b = 1.

    Vậy (E) có bốn đỉnh là : (-2 ; 0), (2 ; 0), (0 ; -1) và (0 ; 1).

    b) Phương trình chính tắc của (E) là : 

    c) (E) có tiêu điểm thứ hai là điểm (√3;0). Đường thẳng Δ đi qua điểm (√3;0) và vuông góc với Ox có phương trình x = √3

    Phương trình tung độ giao điểm của Δ và (E) là :

    Suy ra tọa độ của C và D là : 

    Vậy CD = 1.

Giải bài 7 trang 202 SBT Toán hình lớp 10 tập 1 

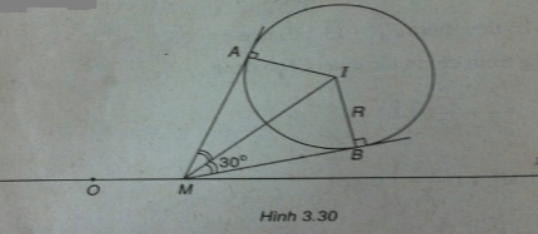
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C): x² + y² - 6x - 6y + 14 = 0. Tìm điểm M thuộc trục hoành sao cho từ M kẻ được hai tiếp tuyến của (C) mà góc giữa hai tiếp tuyến đó bằng 60^ο

Lời giải:

    (Xem hình 3.30)

    Đường tròn (C) có tâm I(3 ; 3) và có bán kính

    Điểm M(x;0) thuộc Ox.

    Từ M kẻ hai tiếp tuyến tiếp xúc với (C) tại A và B. Ta có:

    Vậy có hai điểm M thỏa mãn đề bài, chúng có tọa độ là: M₁(3 + √7;0) và M₂(3 - √7;0)

Giải bài 8 SBT Toán hình 10 tập 1 trang 202

Cho đường tròn (C) tâm I(1;-2), bán kính R và điểm K(1;3).

     a) Cho R = 1. Viết phương trình tiếp tuyến của (C) đi qua K;

     b) Xác định R để từ K vẽ được đến (C) hai tiếp tuyến tiếp xúc với (C) lần lượt tại hai điểm M₁, M₂ sao cho diện tích tứ giác KM₁IM₂ bằng 2√6 .

Lời giải:

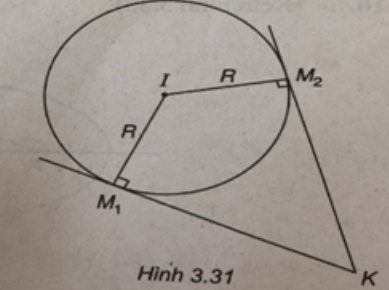
     (Xem hình 3.31)

     a) R = 1. Gọi Δ là đường thẳng đi qua điểm K(1 ; 3) và có hệ số góc m. Δ có phương trình y = m(x - 1) + 3

     ⇔ mx - y + (3 - m) = 0.

     Ta có Δ tiếp xúc vơi (C) ⇔ d(I,Δ) = R

     Vậy qua điểm K có hai tiếp tuyến với (C). Đó là :

     Δ₁: y = 2√6(x - 1) + 3 và Δ₂: y = -2√6(x - 1) + 3

     b) Ta có: 

     Ta có: S_KM1IM2 = 2√6

     ⇔ 2S_IM2K = 2√6

     ⇔ IM₂. KM₂ = 2√6

     ⇔ R²(25 - R²) = 24

     ⇔ R⁴ - 25R² + 24 = 0

     Vậy bán kính đường tròn bằng 1 hoặc 2√6.

Giải sách bài tập Toán hình 10 tập 1 bài 9 trang 202

Trong mặt phẳng tọa độ Oxy, cho đường tròn (C): (x - 5)² + (y - 3)² = 4 và điểm A(1;2), một đường thẳng d đi qua A và cắt đường tròn (C) theo một dây cung MN có độ dài bằng 2√3. Viết phương trình của d.

Lời giải:

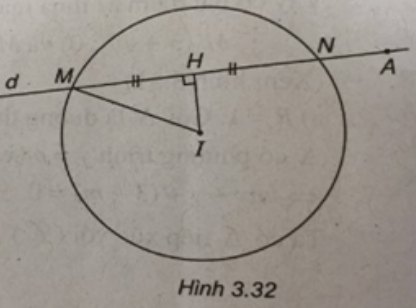
    (Xem hình 3.32)

    Đường tròn (C) có tâm I(5 ; 3) và có bán kính R = 2.

    Gọi H là trung điểm của MN. Ta có

    Phương trình đường thẳng d có dạng: y - 2 = k(x - 1) ⇔ kx - y + 2 = 0.

    Ta có IH = 1

    Vậy có hai điểm d thỏa mãn đề bài.

    Đó là d₁: y - 2 = 0 và d₂: 8x - 15y + 22 = 0

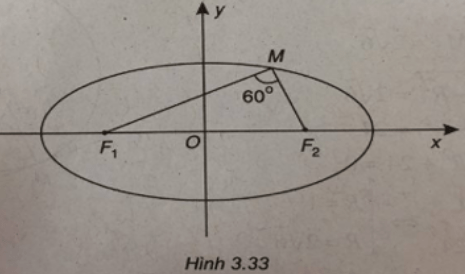
Giải bài 10 trang 202 SBT Toán hình 10 tập 1

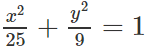
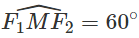
Trong mặt phẳng tọa độ Oxy, cho elip (E):  . Gọi hai tiêu điểm của (E) lần lượt là F₁, F₂ và M thuộc (E) sao cho  . Tìm tọa độ điểm M và tính diện tích tam giác MF₁F₂

Lời giải:

    (Xem hình 3.33)

    Elip (E) có phương trình chính tắc: 

    Ta có : a = 5, b = 3. Suy ra c² = a² - b² = 25 - 9 = 16

    Vậy c = 4.

    Xét điểm M(x;y) thuộc elip, ta có:

    Áp dụng định lí côsin trong tam giác F₁MF₂ ta có:

    Ta lại có: M ∈ (E) ⇒ 

    Thay (1) vào phương trình (2) ta được:

    Vậy có bốn điểm M thỏa mãn đề bài.

    Chúng có tọa độ là 

Giải bài 11 SBT Toán hình 10 tập 1 trang 202

Trong mặt phẳng tọa độ Oxy, cho ba điểm I(2;4), B(1;1), C(5;5). Tìm điểm A sao cho I là tâm đường tròn nội tiếp tam giác ABC.

Lời giải:

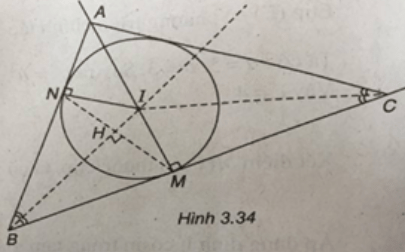
    (Xem hình 3.34)

    Ta có: 

    IB = IC ⇒ AB = AC

    Gọi M là trung điểm của BC, ta có M(3 ; 3).

    Phương trình đường thẳng IM: x + y - 6 = 0 (1)

    Phương trình đường thẳng IB: 3x - y - 2 = 0 (2)

    Gọi N là điểm đối xứng với M qua đường thẳng IB. Đặt N(x;y), ta có tọa độ trung điểm H của MN là 

    Ta có: 

    Ta có B(1;1). Phương trình đường thẳng BN: 7x + y - 8 = 0.

    Điểm A là giao của hai đường thẳng BN và IM nên tọa độ của A là nghiệm của hệ phương trình

    Vậy tọa độ điểm A là 

Giải SBT Toán hình học lớp 10 tập 1 bài 12 trang 202

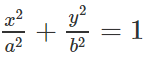
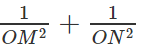
Trong mặt phẳng tọa độ Oxy, cho elip (E):  Một góc vuông uOv (vuông tại O) quay quanh gốc O, cắt elip (E) tại M và N. Chứng minh rằng  không đổi, từ đó suy ra MN luôn tiếp xúc với một đường tròn cố định.

Lời giải:

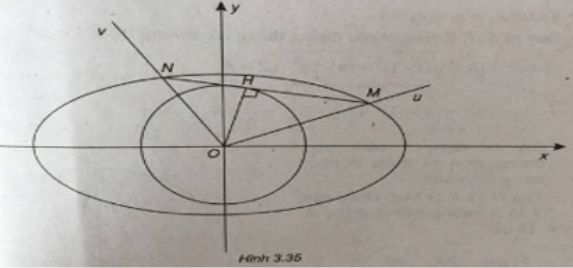
    (Xem hình 3.35)

    Gọi y = kx và y = -x/k là phương trình của Ou và Ov.

    Phương trình hoành độ giao điểm của Ou và elip (E):

    Ta có: 

    Suy ra : 

    Tương tự: 

    Suy ra: 

    Vậy 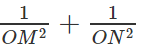 không đổi.

    Vẽ đường cao OH của tam giác vuông OMN.

    Ta có: 

    Suy ra: 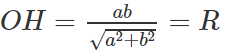 không đổi

    Vậy MN luôn tiếp xúc với đường tròn cố định tâ O bán kính 

Giải bài 13 SBT Toán hình 10 tập 1 trang 202

Trong mặt phẳng tọa độ Oxy, cho đường tròn (C): (x - 1)² + (y - 2)² = 4 và hai điểm A(1 ; 4), B(1; 1/2). Viết phương trình đường thẳng d đi qua B cắt đường tròn (C) tại M, N sao cho AMN có diện tích lớn nhất.

Lời giải:

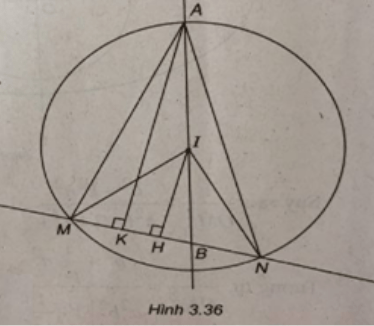
    (Xem hình 3.36)

    Đường tròn (C) có tâm I(1;2) và có bán kính R = 2.

    Ta có: x_A = x_I = x^B

    Suy ra A, I, B cùng thuộc đường thẳng có phương trình x = 1.

    Ta có: 

    Suy ra điểm A nằm trên đường tròn và điểm B nằm trong hình tròn.

    Gọi H và K là hình chiếu của I và A xuống đường thẳng d.

    Ta có: 

    Suy ra S_AMN = 7S_IMN/3

    = (7/3). (1/2). IM. IN. sin MIN = (14/3).sin MIN ≤ 14/3

    S_AMNlớn nhất ⇔ sin MIN = 1 ⇔ góc MIN = 90^ο

    ⇔ IH = (R√2)/2 ⇔ d(I,MN) = √2

    Phương trình đường thẳng MN là :

    y - 0,5 = k(x - 1) ⇔ 2kx - 2y + (1 - 2k) = 0

    Ta có: d(I,MN) = √2

    Vậy phương trình đường thẳng d là:

Giải sách bài tập Toán hình 10 tập 1 bài 14 trang 203

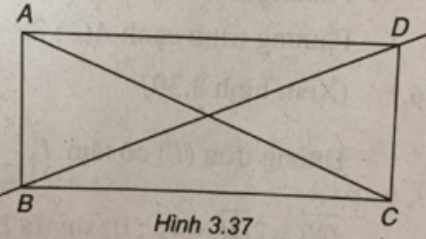
Trong mặt phẳng tọa độ Oxy, cho hình chữ nhật biết tọa độ hai đỉnh đối diện là (1;-5) và (6;2), phương trình của một đường chéo là 5x + 7y - 7 = 0. Tìm tọa độ các đỉnh còn lại của hình chữ nhật.

Lời giải:

    (Xem hình 3.37)

    Đặt A(1 ; -5), C(6 ; 2) và BD có phương trình: 5x + 7y - 7 = 0.

    Đặt x_B = 7t ta có y_B = 1 - 5t.

    Vậy B(7t; 1 - 5t).

    Suy ra: vectơ BA = (1 - 7t; -6 + 5t) và vectơ BC = (6 - 7t; 1 + 5t).

    Ta có: 

    ⇔ (1 - 7t)(6 - 7t) + (1 + 5t)(-6 + 5t) = 0

    Vậy B(0;1); D(7;-4) hoặc B(7;-4); D(0;1).

Giải Toán hình lớp 10 SBT tập 1 bài 15 trang 203

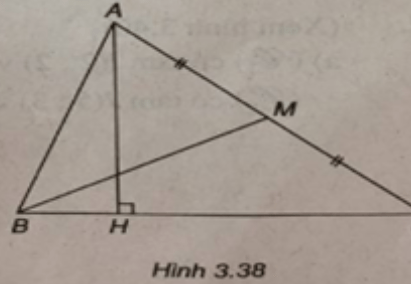
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có AB: 3x + 5y - 33 = 0; đường cao AH: 7x + y - 13 = 0; trung tuyến BM: x + 6y - 24 = 0 (M là trung điểm của AC). Tìm phương trình các cạnh còn lại của tam giác.

Lời giải:

    (Xem hình 3.38)

    Tọa độ điểm A là nghiệm của hệ phương trình:

    Vậy A(1 ; 6)

    Tọa độ điểm B là nghiệm của hệ phương trình:

    Vậy B(6 ; 3).

    Đặt C(x;y) ta suy ra trung điểm M của AC có tọa độ 

    Ta có: vectơ BC(x - 6; y - 3) và vectơ u_AH(1; -7)

    Ta có: 

    Suy ra tọa độ điểm C là nghiệm của hệ phương trình:

    Vậy C(-1 ; 2).

    Phương trình cạnh BC: x - 7y + 15 = 0

    Phương trình cạnh AC: 2x - y + 4 = 0.

Giải bài 16 trang 203 SBT Toán hình 10 tập 1

Trong mặt phẳng với hệ tọa độ Oxy, cho hình chữ nhật có một đỉnh là O, diện tích bằng 12 và đường tròn ngoại tiếp (T) của có có phương trình là 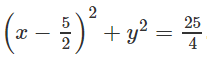 . Tìm tọa độ các đỉnh còn lại của hình chữ nhật.

Lời giải:

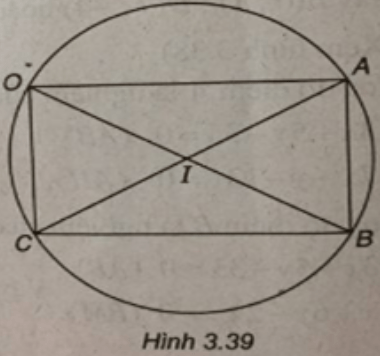
    (Xem hình 3.39)

    Đường tròn (T) có tâm T(5/2; 0) và bán kính R = 5/2.

     = (5;0) suy ra B(5 ; 0). Đặt A(x ; y) ta có hệ phương trình:

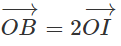
    Vậy ta được: 

Giải SBT Toán hình học lớp 10 tập 1 bài 17 trang 203

Trong mặt phẳng tọa độ Oxy, cho hai đường tròn:

    • (C₁): (x - 2)² + (y - 2)² = 4

    • (C₂): (x - 5)² + (y - 3)² = 16

    a) Chứng minh rằng hai đường tròn (C₁) , (C₂) cắt nhau ;

    b) Tìm tọa độ giao điểm của hai tiếp tuyến chung của (C₁) và (C₂).

Lời giải:

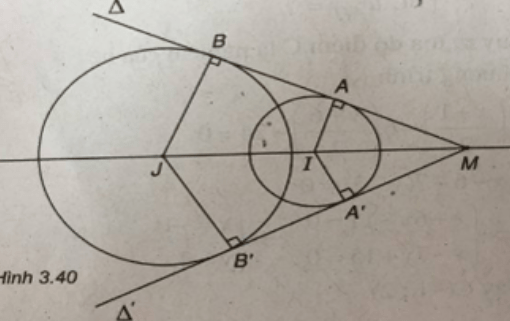
    (Xem hình 3.40)

    a)

    • (C₁) có tâm I(2;2) và bán kính R₁ = 2

    • (C₂) có tâm J(5;3) và bán kính R₂ = 4

    Ta có:

    Do: R₂ - R₁ < IJ < R₂ + R₁

    Nên (C₁) và (C₂) cắt nhau tại hai điểm phân biệt.

    b) Gọi Δ và Δ′ là hai tiếp tuyến chung của (C₁) và (C₂) . Δ tiếp xúc với (C₁) và (C₂) lần lượt tại A, B. Δ′ tiếp xúc với (C₁) và (C₂) lần lượt tại A', B'.

    Ta có:

 

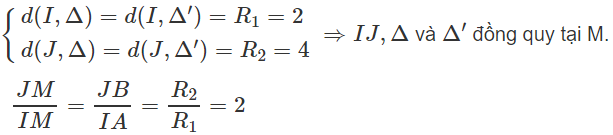
    Vậy ta được M(-1;1).

Giải bài 18 sách bài tập Toán hình 10 tập 1 trang 203

Trong mặt phẳng tọa độ Oxy, cho elip (E): 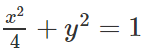 và điểm A(-1; 0,5). Gọi d là đưởng thẳng đi qua A có hệ số góc là m. Xác định m để d cắt (E) tại hai điểm phân biệt M và N sao cho A là trung điểm của MN.

Lời giải:

    Phương trình đường thẳng d có dạng: y - 0,5 = m(x + 1) ⇔ y = m(x + 1) + 0,5.

    Phương trình hoành độ giao điểm của d và (E) là:

    x²/4 + (mx + m + 0,5)² = 1

    ⇔ x² + 4[mx + (m + 0,5)]² = 4

    ⇔ (4m² + 1)x² + 4[(2m + 1)m]x + 4(m + 0,5)² - 4 = 0

    A là trung điểm của MN

    ⇔ 4m² + 2m = 4m² + 1 ⇔ m = 0,5

Giải bài 19 trang 203 SBT Toán hình lớp 10 tập 1 

Trong mặt phẳng Oxy, cho hình chữ nhật ABCD có đỉnh A(2;-1), phương trình một đường chéo là x - 7y + 15 = 0 và độ dài cạnh AB = 3√2. Tìm tọa độ các đỉnh A, C, D biết y_B là một số nguyên.

Lời giải:

    Do tọa độ A không thỏa mãn phương trình đường thẳng x - 7y + 15 = 0 nên phương trình đường chéo BD là : x - 7y + 15 = 0, tọa độ điểm B là B(7t - 15; t).

    Ta có :

    AB = 3√2 ⇔ (7t - 17)² + (t + 1)² = 18

    ⇔ 50t² - 236t + 272 = 0

    ( (∗) loại)

    Vậy B(-1 ; 2)

    Ta có: 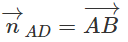 = (-3;3) = -3(1;-1)

    Phương trình đường thẳng AD là :

    1(x - 2) - 1(y + 1) = 0

    ⇔ x - y - 3 = 0

    Tọa độ điểm D là nghiệm của hệ:

    Vậy D(6 ; 3).

    Ta có AC và BD cắt nhau tại trung điểm I.

    Suy ra:

    Vậy C(3 ; 6).

Giải bài 20 SBT Toán hình 10 tập 1 trang 203

Trong mặt phẳng tọa độ Oxy, cho hai đường tròn: (C₁): x² + y² + 10x = 0 và (C₂): x² + y² - 4x - 2y - 20 = 0 có tâm lần lượt là I, J.

    a) Viết phương trình đường tròn (C) đi qua giao điểm của (C₁) , (C₂) và có tâm nằm trên đường thẳng d: x - 6y + 6 = 0.

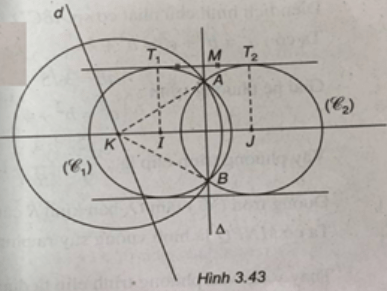
    b) Viết phương trình tiếp tuyến chung của (C₁) và (C₂). Gọi T₁, T₂ lần lượt là tiếp điểm của (C₁) , (C₂) với một tiếp tuyến chung, hãy viết phương trình đường thẳng Δ qua trung điểm của T₁T₂ và vuông góc với IJ.

Lời giải:

    (Xem hình 3.43)

    a) (C₁) có tâm I(-5;0), bán kính R₁ = 5. (C₂) có tâm I(2;1), bán kính R₂ = 5

    Tọa độ của giao điểm A, B của (C₁) và (C₂) là nghiệm của hệ phương trình:

    Ta được A(-1 ; -3), B(-2 ; 4).

    Gọi K là tâm của (C) ta có KA = KB = R ⇒ K ∈ IJ.

    Phương trình IJ là: x - 7y + 5 = 0.

    Tọa độ K là nghiệm của hệ phương trình:

    Vậy K(-12 ; -1). Ta có R₂ = KA₂ = 125.

    Vậy phương trình của đường tròn (C) là : (x + 12)² + (y + 1)² = 125.

    b) R₁ = R₂ = 5 ⇒ tiếp tuyến chung l của (C₁) và (C₂) song song với IJ. Phương trình l có dạng: x - 7y + c = 0.

    Ta có: d(I,l) = R₁

    Vậy phương trình của hai tiếp tuyến chung của (C₁) và (C₂) là :

    Đường thẳng AB đi qua trung điểm M của T₁T₂và vuông góc với IJ.

    Phương trình của AB là: 7x + y + 10 = 0.

Giải sách bài tập Toán hình 10 tập 1 bài 21 trang 204

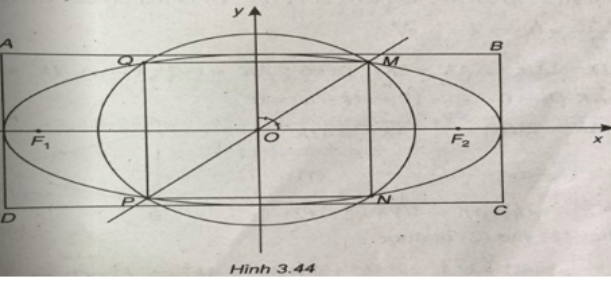
Trong mặt phẳng tọa độ Oxy, lập phương trình chính tắc của elip (E) biết (E) có tiêu điểm F₁(-2;0) và diện tích hình chữ nhật cơ sở bằng 12√5

    Viết phương trình đường tròn (C) có tâm là gốc tọa độ và (C) cắt (E) tại bốn điểm tạo thành hình vuông.

Lời giải:

    (Xem hình 3.44)

    Phương trình elip (E) có dạng: 

    Ta có tiêu điểm F₁(-2;0). Suy ra c = 2.

    Diện tích hình chữ nhật cơ sở ABCD là 4ab. Suy ra 4ab = 12√5

    Ta có : a² = b² + c² = b² + 4.

    Giải hệ phương trình :

    Ta được:

    Vậy phương trình elip là: 

    Đường tròn (C) tâm O, bán kính R cắt elip tại bốn điểm M, N, P, Q.

    Ta có MNPQ là hình vuông suy ra phương trình đường thẳng OM là : y = x.

    Thay y = x vào phương trình elip ta được:

    Vậy phương trình đường tròn (C) là : 

Giải bài 22 trang 204 SBT Toán hình 10 tập 1 

Trong mặt phẳng tọa độ Oxy, cho hình chữ nhật ABCD có x_A = 2, điểm C và trung điểm K của AD cùng thuộc trục Oy, tâm I thuộc trục Ox, AD = 2AB. Tìm tọa độ các đỉnh của hình chữ nhật ABCD, biết rằng K có tung độ âm.

Lời giải:

    Đặt A(2; a), K(0; k), C(0; c), I(1; 0) là tọa độ các điểm đã cho ta có:

    AD = 2AB ⇒ AK = 2KI.

    Ta có: 

    Thay (1) vào (2) ta được:

    Suy ra a = -3.

    Vậy A(2;-3), C(0;3) và K(0;-1).

    Ta có:

    Vậy D(-2;1)

    Ta có:

    Vậy B(4;-1).

CLICK NGAY vào nút TẢI VỀ dưới đây để download Giải sách bài tập Toán lớp 10 tập 1 trang 201, 202, 203, 204 file word, pdf hoàn toàn miễn phí.