Giải SBT Toán 10 trang 109, 110, 111 tập 1 bài 2 chương 4 đầy đủ nhất

Giải sách bài tập Toán 10 tập 1 bài 2 chương 4: Bất phương trình và hệ bất phương trình một ẩn được giải đáp chi tiết và rõ ràng nhất, giúp cho các bạn học sinh có thể tham khảo và chuẩn bị tốt nhất cho bài học sắp tới nhé.

Giải bài 15 SBT Toán lớp 10 tập 1 trang 109

Viết điều kiện của mỗi bất phương trình sau:

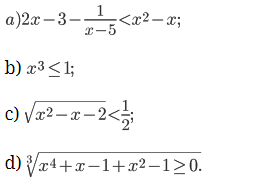
Lời giải:

a) Điều kiện là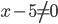 

b) Điều kiện là x tùy ý.

c) Điều kiện là x² - x  - 2>= 0 

d) Điều kiện là x tùy ý.

Giải sách bài tập Toán 10 tập 1 bài 16 trang 110

Chứng tỏ rằng x = -7 không phải là nghiệm của bất phương trình 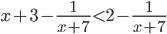 nhưng lại là nghiệm của bất phương trình x + 3 < 2.

Lời giải:

làm hai vế của bất phương trình đầu vô nghĩa nên x = -7 không là nghiệm của bất phương trình đó. Mặt khác, x = -7 thỏa mãn bất phương trình sau nên x = -7 là nghiệm của bất phương trình này.

Nhận xét: Phép giản ước số hạng 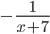 ở hai vế của bất phương trình đầu làm mở rộng tập xác định của bất phương trình đó, vì vậy có thể dẫn đến nghiệm ngoại lai.

Giải Toán lớp 10 SBT tập 1 bài 17 trang 110

Xét xem x = -3 là nghiệm của bất phương trình nào trong hai bất phương trình sau 3x + 1 < x + 3 (1) và (3x + 1)² < (x + 3)² (2)

Từ đó suy ra rằng phép bình phương hai vế một bất phương trình không phải là phép biến đổi tương đương.

Lời giải:

Thử trực tiếp ta thấy ngay x = -3 là nghiệm của bất phương trình (1) nhưng không là nghiệm bất phương trình (2), vì vậy (1) và (2) không tương đương do đó phép bình phương hai vế một bất phương trình không phải là phép biến đổi tương đương.

Giải bài 18 trang 110 SBT Toán 10 tập 1

Viết điều kiện của mỗi bất phương trình đã cho sau đây rồi cho biết các bất phương trình này có tương đương đương với nhau hay không:

Hai bất phương trình đã cho không tương đương với nhau vì có x = -1 là một nghiệm của (1) nhưng không là nghiệm của (2).

Nhận xét: Phép biến đổi đồng nhất 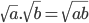 làm mở rộng tập xác định, dẫn tới thay đổi điều kiện của phương trình, do đó có thể làm xuất hiện nghiệm ngoại lai.

Giải SBT Toán lớp 10 tập 1 bài 19 trang 110

Nếu nhân hai vế bất phương trình 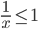 với x ta được bất phương trình nào? Bất phương trình nhận được có tương đương với bất phương trình đã cho hay không? Vì sao?

Gợi ý làm bài

Nếu nhân hai vế của 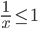 với x, ta được bất phương trình mới x≥1; bất phương trình này không tương đương với bất phương trình đã cho vì đã làm mất đi tất cả các nghiệm âm của nó.

Ghi nhớ: Không được nhân hay chia hai vế của một bất phương trình với một biểu thức chứa ẩn mà không biết dấu của biểu thức đó.

Giải sách bài tập Toán 10 tập 1 bài 20 trang 110

Nếu bình phương hai vế (khử căn thức chứa ẩn) của bất phương trình 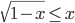 ta nhận được bất phương trình nào? Bất phương trình nhận được có tương đương với bất phương trình đã cho hay không? Vì sao?

Lời giải:

Nếu bình phương hai vế (khử căn thức chứa ẩn) của bất phương trình 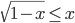 ta nhận được bất phương trình 1- x <= x² 

Bất phương trình nhận được không tương đương với bất phương trình đã cho vì có x = 2 không phải là nghiệm bất phương trình đã cho nhưng lại là nghiệm của bất phương trình mới nhận được sau phép bình phương.

Ghi nhớ: Không được bình phương hai vế một bất phương trình vì có thể làm xuất hiện nghiệm ngoại lai.

Giải bài 21 SBT Toán 10 tập 1 trang 110

Hãy viết điều kiện của bất phương trình sau rồi suy ra rằng bất phương trình đó vô nghiệm.

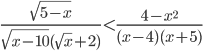
Lời giải:

Điều kiện của bất phương trình đã cho là:

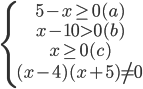
Nếu x là một nghiệm của bất phương trình đã cho thì trước hết x phải thỏa mãn (a) và (b), suy ra (5 - x) + (x - 10) > 0 , do đó -5 > 0, vô lí. Vì vậy bất phương trình đã cho vô nghiệm.

Giải bài 22 sách bài tập Toán 10 tập 1 trang 110

Chứng minh rằng các bất phương trình sau đây vô nghiệm:

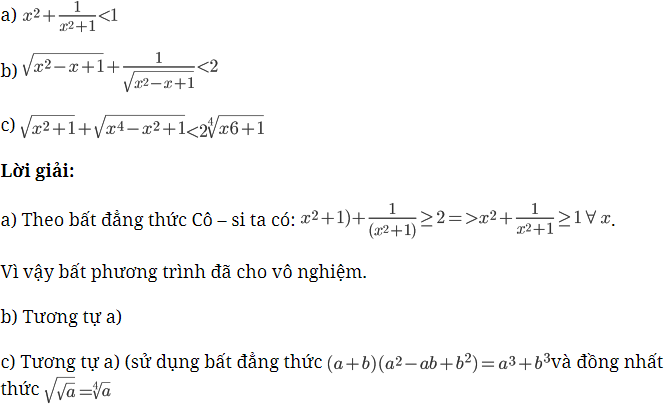
Giải Toán lớp 10 SBT tập 1 bài 23 trang 110

Giải các bất phương trình sau:

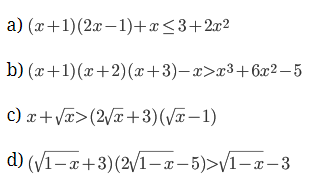
Lời giải:

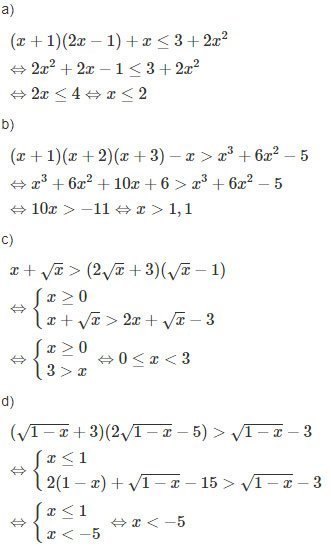
Giải bài 24 sách bài tập Toán 10 tập 1 trang 111

Giải các bất phương trình sau:

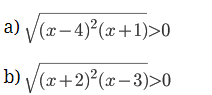
Lời giải:

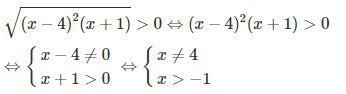
Tập nghiệm của bất phương trình là: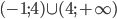 

b) Đáp số: x > 3.

Bài 25 trang 111 Sách bài tập Toán tập 1 lớp 10

Giải các bất phương trình sau:

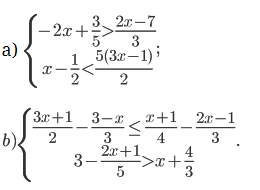
Lời giải:

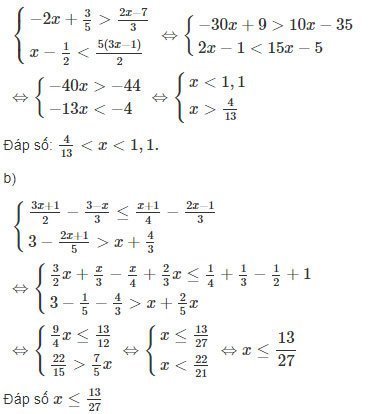
Giải SBT Toán 10 tập 1 bài 26 trang 111

Giải và biện luận bất phương trình theo tham số m.

mx - m² > 2x -4

Lời giải:

mx - m² > 2x - 4 ⇔ (m - 2)x > (m - 2) (m + 2)

Nếu m > 2 thì m – 2 > 0, bất phương trình có nghiệm là x > m + 2;

Nếu m < 2 thì m – 2 < 0, bất phương trình có nghiệm là x < m + 2;

Nếu m = 2 thì bất phương trình trở thành 0x > 0, bất phương trình vô nghiệm.

CLICK NGAY vào nút TẢI VỀ dưới đây để download Giải sách bài tập Toán lớp 10 tập 1 trang 109, 110, 111 file word, pdf hoàn toàn miễn phí.