Logo

Giải SBT Toán hình học 10 trang 23 tập 1: Tổng và hiệu của hai vec tơ

Giải SBT Toán hình lớp 10 trang 23 tập 1 bài 2 chương 1: Tổng và hiệu của hai vec tơ đầy đủ hỗ trợ các em học sinh củng cố kiến thức và hiểu rõ phương pháp giải các dạng bài tập trong sách bài tập
3.0
1 lượt đánh giá

Nội dung bài viết

  1. Giải bài 1.8 SBT Toán hình 10 tập 1 trang 23
  2. Giải sách bài tập Toán hình 10 tập 1 bài 1.9 trang 23
  3. Giải Toán hình học lớp 10 SBT tập 1 bài 1.10 trang 23
  4. Giải bài 1.11 trang 23 SBT Toán hình 10 tập 1
  5. Giải SBT Toán hình học lớp 10 tập 1 bài 1.12 trang 23
  6. Giải bài 1.13 sách bài tập Toán hình 10 tập 1 trang 23
  7. Giải bài 1.14 trang 23 SBT Toán hình lớp 10 tập 1 
  8. Giải bài 1.15 SBT Toán hình 10 tập 1 trang 23
  9. Giải sách bài tập Toán hình 10 tập 1 bài 1.16 trang 23
  10. Giải bài 1.17 trang 23 SBT Toán hình 10 tập 1
  11. Giải SBT Toán hình học lớp 10 tập 1 bài 1.18 trang 23
  12. Giải bài 1.19 SBT Toán hình 10 tập 1 trang 23

Giải sách bài tập Toán 10 tập 1 bài 2 chương 1: Tổng và hiệu của hai vec tơ được giải đáp chi tiết và rõ ràng nhất, giúp cho các bạn học sinh có thể tham khảo và chuẩn bị tốt nhất cho bài học sắp tới nhé.

Giải bài 1.8 SBT Toán hình 10 tập 1 trang 23

Cho năm điểm A, B, C, D và E. Hãy xác định tổng \underset{AB}{\rightarrow} + \underset{BC}{\rightarrow} + \underset{CD}{\rightarrow} +\underset{DE}{\rightarrow}

Lời giải:

\underset{AB}{\rightarrow}+\underset{BC}{\rightarrow}+\underset{CD}{\rightarrow}+\underset{DE}{\rightarrow}=\underset{AC}{\rightarrow}+\underset{CD}{\rightarrow}+\underset{DE}{\rightarrow}

=\underset{AD}{\rightarrow}+\underset{DE}{\rightarrow}=\underset{AE}{\rightarrow}

Giải sách bài tập Toán hình 10 tập 1 bài 1.9 trang 23

Cho bốn điểm A, B, C và D. Chứng minh \underset{AB}{\rightarrow}-\underset{CD}{\rightarrow}=\underset{AC}{\rightarrow}-\underset{BD}{\rightarrow}

Lời giải:

 \underset{AB}{\rightarrow}-\underset{CD}{\rightarrow}=\underset{AC}{\rightarrow}-\underset{BD}{\rightarrow}

⇔\underset{AB}{\rightarrow}+\underset{BD}{\rightarrow}=\underset{AC}{\rightarrow}+\underset{CD}{\rightarrow}

⇔\underset{AD}{\rightarrow}=\underset{AD}{\rightarrow}

Giải Toán hình học lớp 10 SBT tập 1 bài 1.10 trang 23

Cho hai vec tơ \underset{a}{\rightarrow} và \underset{b}{\rightarrow} sao cho \underset{a}{\rightarrow}+\underset{b}{\rightarrow}= \underset{0}{\rightarrow}

a) Dựng \underset{OA}{\rightarrow}=\underset{a}{\rightarrow},\underset{OB}{\rightarrow}=\underset{b}{\rightarrow}. Chứng minh O là trung điểm của AB.

b) Dựng \underset{OA}{\rightarrow}=\underset{a}{\rightarrow}, \underset{AB}{\rightarrow}=\underset{b}{\rightarrow}. Chứng minh O≡B

Lời giải:

\underset{OA}{\rightarrow}-\underset{OB}{\rightarrow}=\underset{0}{\rightarrow}=>\underset{OB}{\rightarrow}=−\underset{OA}{\rightarrow}=>OB=OA ba điểm A, O, B thẳng hàng và điểm O ở giữa A và B. Suy ra O là trung điểm của AB.

b)

\underset{OA}{\rightarrow}+\underset{OB}{\rightarrow}=\underset{0}{\rightarrow}=>\underset{OB}{\rightarrow}=\underset{0}{\rightarrow}=>B≡O

Giải bài 1.11 trang 23 SBT Toán hình 10 tập 1

Gọi O là tâm của tam giác đều ABC. Chứng minh rằng

\underset{OA}{\rightarrow}+\underset{OB}{\rightarrow}+\underset{OC}{\rightarrow}=\underset{0}{\rightarrow}

Lời giải:

Trong tam giác đều ABC, tâm O của đường tròn ngoại tiếp cũng là trọng tâm của tam giác. Vậy

\underset{OA}{\rightarrow}+\underset{OB}{\rightarrow}+\underset{OC}{\rightarrow}=\underset{0}{\rightarrow}

Giải SBT Toán hình học lớp 10 tập 1 bài 1.12 trang 23

Gọi O là giao điểm hai đường chéo của hình bình hành ABCD. Chứng minh rằng

\underset{OA}{\rightarrow}+\underset{OB}{\rightarrow}+\underset{OC}{\rightarrow}+\underset{OD}{\rightarrow}=\underset{0}{\rightarrow}

Lời giải:

\underset{OA}{\rightarrow}+\underset{OB}{\rightarrow}+\underset{OC}{\rightarrow}+\underset{OD}{\rightarrow}=(\underset{OA}{\rightarrow}+\underset{OC}{\rightarrow})+(\underset{OB}{\rightarrow}+\underset{OD}{\rightarrow})

=\underset{0}{\rightarrow}+\underset{0}{\rightarrow}=\underset{0}{\rightarrow}

Giải bài 1.13 sách bài tập Toán hình 10 tập 1 trang 23

Cho tam giác ABC có trung tuyến AM. Trên cạnh AC lấy hai điểm E và F sao cho AE = EF= FC; BE cắt AM tại N. Chứng minh \underset{NA}{\rightarrow} và \underset{NM}{\rightarrow} là hai vec tơ đối nhau.

Lời giải:

(h. 1.41)

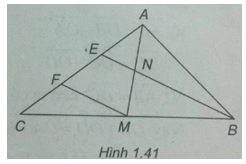
Giải bài tập Toán 10 SBT bài 2 chương 1 phần Hình học

FM // BE vì FM là đường trung bình của tam giác CEB.

Ta có EA = EF. Vậy EN là đường trung bình của tam giác AFM. Vậy \underset{NA}{\rightarrow} =−\underset{NM}{\rightarrow}

Giải bài 1.14 trang 23 SBT Toán hình lớp 10 tập 1 

Cho hai điểm phân biệt A và B. Tìm điểm M thỏa mãn một trong các điều kiện sau:

a) \underset{MA}{\rightarrow}-\underset{MB}{\rightarrow}=\underset{BA}{\rightarrow}

b) \underset{MA}{\rightarrow}-\underset{MB}{\rightarrow}=\underset{AB}{\rightarrow}

c) \underset{MA}{\rightarrow}+\underset{MB}{\rightarrow}=\underset{0}{\rightarrow}

Lời giải:

a)\underset{MA}{\rightarrow}-\underset{MB}{\rightarrow}=\underset{BA}{\rightarrow}⇔\underset{BA}{\rightarrow}=\underset{BA}{\rightarrow}. Vậy mọi điểm M đều thỏa mãn hệ thức a).
b) \underset{MA}{\rightarrow}-\underset{MB}{\rightarrow}=\underset{AB}{\rightarrow}⇔\underset{BA}{\rightarrow}=\underset{AB}{\rightarrow}⇔A=B. Vô lí. Vậy không có điểm M nào thỏa mãn hệ thức

c) \underset{MA}{\rightarrow}+\underset{MB}{\rightarrow}=\underset{0}{\rightarrow}⇔\underset{MA}{\rightarrow}=-\underset{MB}{\rightarrow}. Vậy M là trung điểm của đoạn thẳng AB.

Giải bài 1.15 SBT Toán hình 10 tập 1 trang 23

Cho tam giác ABC. Chứng minh rằng nếu \left | \vec{CA}-\vec{CB} \right | =\left | \vec{CA}-\vec{CB} \right | thì tam giác ACB là tam giác vuông cân tại C.

Lời giải:

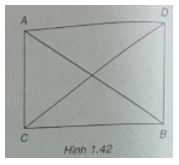
Vẽ hình bình hành CADB.

Ta có \underset{CA}{\rightarrow}+\underset{CB}{\rightarrow}=\underset{CD}{\rightarrow}, do đó \left | \vec{CA}+\vec{CB} \right | =CD

Vì \underset{CA}{\rightarrow}-\underset{CB}{\rightarrow}=\underset{BA}{\rightarrow}, do đó \left | \vec{CA}-\vec{CB} \right | =BA

Từ \left | \vec{CA}+\vec{CB} \right | =\left | \vec{CA}-\vec{CB} \right |

suy ra CD = AB (h.1.42)

Vậy tứ giác CADB là hình chữ nhật. Ta có tam giác ACB vuông tại C.

Giải bài tập Toán 10 SBT bài 2 chương 1 phần Hình học

Giải sách bài tập Toán hình 10 tập 1 bài 1.16 trang 23

Cho ngũ giác ABCDE. Chứng minh \underset{AB}{\rightarrow}+\underset{BC}{\rightarrow}+\underset{CD}{\rightarrow}=\underset{AE}{\rightarrow}-\underset{DE}{\rightarrow}

Lời giải:

\underset{AB}{\rightarrow}+\underset{BC}{\rightarrow}+\underset{CD}{\rightarrow}=\underset{AE}{\rightarrow}-\underset{DE}{\rightarrow}

⇔ \underset{AC}{\rightarrow}+\underset{CD}{\rightarrow}=\underset{AE}{\rightarrow}+\underset{ED}{\rightarrow}

⇔ \underset{AD}{\rightarrow}=\underset{AD}{\rightarrow}

Giải bài 1.17 trang 23 SBT Toán hình 10 tập 1

Cho ba điểm O, A, B không thẳng hàng. Với điều kiện nào thì vec tơ \underset{OA}{\rightarrow}+\underset{OB}{\rightarrow} nằm trên đường phân giác của góc \hat{AOB}?

Gợi ý làm bài

\underset{OA}{\rightarrow}+\underset{OB}{\rightarrow}=\underset{OC}{\rightarrow} trong đó OACB là hình bình hành. OC là phân giác góc\hat{AOB} khi và chỉ khi OACB là hình thoi, tức là OA = OB.

Giải SBT Toán hình học lớp 10 tập 1 bài 1.18 trang 23

Cho hai lực \vec{F_{1} } và \vec{F_{2} } có điểm đặt O và tạo với nhau góc 600. Tìm cường độ tổng hợp lực của hai lực ấy biết rằng cường độ của hai lực \vec{F_{1} }và \vec{F_{2} } đều là 100N.

Lời giải:

(h.1.43)

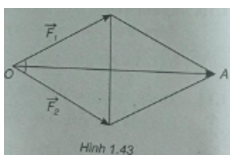
Giải bài tập Toán 10 SBT bài 2 chương 1 phần Hình học

\vec{F_{1} }+\vec{F_{2} }=\vec{F}=\underset{OA}{\rightarrow}

\left | \vec{F_{1} } +\vec{F_{2} } \right |=OA=100\sqrt{3}

Vậy cường độ của hợp lực là 100\sqrt{3}N

Giải bài 1.19 SBT Toán hình 10 tập 1 trang 23

Cho hình bình hành ABCD. Gọi O là một điểm bất kì trên đường chéo AC. Qua O kẻ các đường thẳng song song với các cạnh của hình bình hành. Các đường thẳng này cắt AB và DC lần lượt tại M và N, cắt AD và BC lần lượt tại E và F. Chứng minh rằng:

a) \underset{OA}{\rightarrow}+\underset{OC}{\rightarrow}=\underset{OB}{\rightarrow}-\underset{OD}{\rightarrow}

b) \underset{BD}{\rightarrow}=\underset{ME}{\rightarrow}+\underset{FN}{\rightarrow}

Lời giải:

(Xem h.1.44)

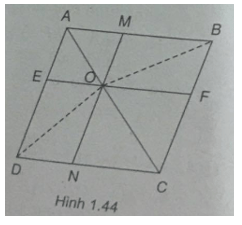
Giải bài tập Toán 10 SBT bài 2 chương 1 phần Hình học

a) \underset{AB}{\rightarrow}=\underset{OB}{\rightarrow}-\underset{OA}{\rightarrow}

\underset{DC}{\rightarrow}=\underset{OC}{\rightarrow}-\underset{OD}{\rightarrow}

Giải bài tập Toán 10 SBT bài 2 chương 1 phần Hình học

CLICK NGAY vào nút TẢI VỀ dưới đây để download Giải sách bài tập Toán lớp 10 tập 1 trang 23 file word, pdf hoàn toàn miễn phí.

Đánh giá bài viết
3.0
1 lượt đánh giá
CÔNG TY CỔ PHẦN TRUYỀN THÔNG HDC VIỆT NAM
Tầng 3, toà nhà S3, Vinhomes Skylake, đường Phạm Hùng, quận Nam Từ Liêm, Hà Nội
Liên hệ quảng cáo: tailieucom123@gmail.com
Copyright © 2020 Tailieu.com
DMCA.com Protection Status