Lời giải Toán Lớp 9 Bài 2: Đường kính và dây của đường tròn

Để quá trình tiếp thu kiến thức mới trở nên dễ dàng và đạt hiệu quả nhất, trước khi bắt đầu bài học mới các em cần có sự chuẩn bị nhất định qua việc tổng hợp nội dung kiến thức lý thuyết trọng tâm, sử dụng những kiến thức hiện có thử áp dụng giải các bài toán, trả lời câu hỏi liên quan. Dưới đây chúng tôi đã soạn sẵn Lời giải Toán Lớp 9 Bài 2: Đường kính và dây của đường tròn đầy đủ nhất, giúp các em tiết kiệm thời gian. Nội dung chi tiết được chia sẻ dưới đây.

Bài 2: Đường kính và dây của đường tròn:

Trả lời câu hỏi:

Câu hỏi trang 103:

Hãy đưa ra một ví dụ để chứng tỏ rằng đường kính đi qua trung điểm của một dây có thể không vuông góc với dây ấy.

Lời giải

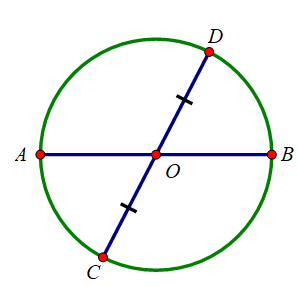
O là trung điểm của CD

AB đi qua trung điểm của CD nhưng AB không vuông góc với CD

Câu hỏi trang 104:

Cho hình 67. Hãy tính độ dài dây AB, biết OA = 13 cm, AM = MB, OM = 5 cm.

Lời giải

OM là 1 phần đường kính đi qua trung điểm của AB

⇒ OM ⊥ AB

Xét tam giác OAM vuông tại M có:

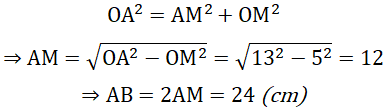
Bài 10 (trang 104 SGK Toán 9 Tập 1):

Cho tam giác ABC, các đường cao BD và CE. Chứng minh rằng:

a) Bốn điểm B, E, D, C cùng thuộc một đường tròn.

b) DE < BC.

Lời giải:

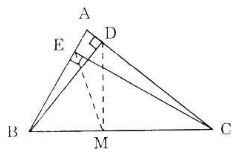
a) Gọi M là trung điểm của BC.

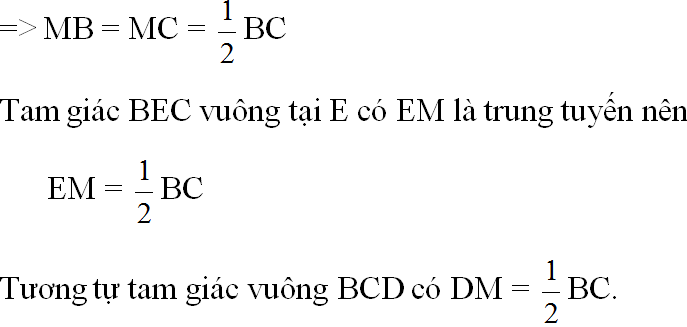
=> ME = MB = MC = MD

Do đó bốn điểm B, E, D, C cùng thuộc đường tròn tâm M. (đpcm)

b) Trong đường tròn tâm M nói trên, ta có DE là dây, BC là đường kính nên DE < BC.

Bài 11 (trang 104 SGK Toán 9 Tập 1):

Cho đường tròn (O) đường kính AB, dây CD không cắt đường kính AB, Gọi H và K theo thứ tự là chân các đường vuông góc kẻ từ A và B đến CD. Chứng minh rằng CH = DK.

Gợi ý: Kẻ OM vuông góc với CD.

Lời giải:

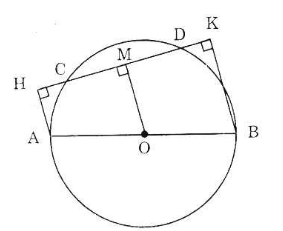
Kẻ OM ⊥ CD.

Vì AH // BK (cùng vuông góc HK) nên tứ giác AHKB là hình thang.

Hình thang AHKB có:

    AO = OB (bán kính).

    OM // AH // BK (cùng vuông góc HK)

=> OM là đường trung bình của hình thang.

=> MH = MK         (1)

Vì OM ⊥ CD nên MC = MD     (2)

Từ (1) và (2) suy ra CH = DK. (đpcm)

Tổng hợp lý thuyết trọng tâm:

1. So sánh độ dài của đường kính và dây.

Trong các dây của một đường tròn, dây lớn nhất là đường kính.

Ví dụ: Gọi AB là một dây bất kỳ của đường tròn (O; R). Chứng minh rằng AB ≤ 2R

+ Trường hợp 1: AB là đường kính

⇒ AB = 2R

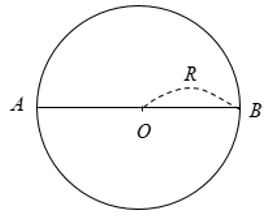
+ Trường hợp 2: AB không là đường kính

Xét tam giác AOB, áp dụng bất đẳng thức tam giác ta có:

AB < AO + OB = R + R = 2R

Vậy ta luôn có AB ≤ 2R

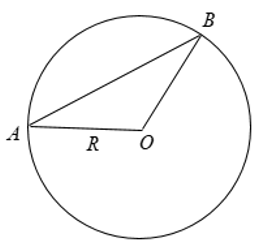
2. Quan hệ vuông góc giữa đường kính và dây.

+ Trong một đường tròn, đường kính vuông góc với dây thì đi qua trung điểm của dây đó.

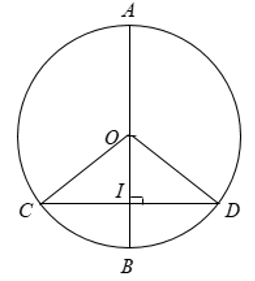
+ Trong một đường tròn, đường kính đi qua trung điểm của một dây không đi qua tâm thì vuông góc với dây ấy.

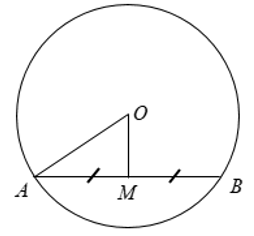
Ví dụ: Cho hình vẽ sau, tính độ dài dây AB khi biết OA = 13cm; AM = MB; OM = 5cm.

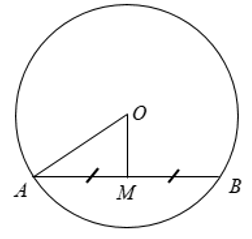
Hướng dẫn:

Áp dụng định lý: “ Trong một đường tròn, đường kính đi qua trung điểm của một dây không đi qua tâm thì vuông góc với dây ấy “

Khi đó ta có: OM ⊥ AB.

Áp dụng định lý Py – ta – go ta có:

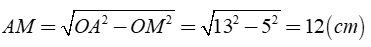
⇒ AB = 2.AM = 2.12 = 24 (cm)

File tải miễn phí lời giải Toán Lớp 9 Bài 2: Đường kính và dây của đường tròn:

Hy vọng tài liệu sẽ hữu ích cho bạn trong quá trình ôn luyện.