Giải Bài: Ôn tập chương 2 Toán 9 (Đại số) đầy đủ nhất

Thực hành giải các bài toán trong phần ôn tập chương sẽ giúp các em tổng hợp lại kiến thức đã học, nắm rõ nội dung lý thuyết và bài tập trọng tâm trong chương thường xuyên được thầy cô đưa vào các bài kiểm tra trên lớp từ đó định hướng phương pháp giải nhanh, ngắn gọn, chính xác sẵn sàng chiến đấu với các bài kiểm tra sắp tới. Dưới đây là hướng dẫn giải chi tiết Bài: Ôn tập chương 2 Hàm số bậc nhất từ đội ngũ chuyên gia giàu kinh nghiệm chia sẻ, mời các em cùng quý thầy cô tham khảo dưới đây.

Ôn tập chương 2 - Hàm số bậc nhất

Câu hỏi ôn tập:

Câu 1 (trang 59 SGK Toán 9 Tập 1): 

Cho hàm số y = ax = b (a ≠ 0).

a) Khi nào thì hàm số đồng biến?

b) Khi nào thì hàm số nghịch biến?

Phương pháp giải:

►Xem lại lý thuyết phần ôn tập chương 2 được chúng tôi chia sẻ cuối bài.

Hướng dẫn giải chi tiết:

a) Hàm số đồng biến khi a > 0

b) Hàm số nghịch biến khi a < 0

Câu 2 (trang 60 SGK Toán 9 Tập 1): 

Khi nào thì hai đường thẳng y = ax + b ( a ≠ 0) và y = a'x + b' (a' ≠ 0) cắt nhau? Song song với nhau? Trùng nhau?

Phương pháp giải:

►Xem lại lý thuyết phần ôn tập chương 2 được chúng tôi chia sẻ cuối bài.

Hướng dẫn giải chi tiết:

Hai đường thẳng y = ax + b và y = a'x + b' (a, a' ≠ 0)

   - Cắt nhau khi và chỉ khi a ≠ a'

   - Song song với nhau khi và chỉ khi a = a', b ≠ b'

   - Trùng nhau khi và chỉ khi a = a', b = b'

Bài tập ôn tập:

Bài 32 (trang 61 SGK Toán 9 Tập 1): 

a) Với những giá trị nào của m thì hàm số bậc nhất y = (m – 1)x + 3 đồng biến?

b) Với những giá trị nào của k thì hàm số bậc nhất y = (5 – k)x + 1 nghịch biến?

Phương pháp giải:

Hàm số có dạng y=ax+b với a≠0 được gọi là hàm số bậc nhất đối với biến số x.

Hàm số bậc nhất y=ax+b xác định với mọi giá trị của x và có tính chất:

Hàm số đồng biến trên R khi a>0

Hàm số nghịch biến trên R khi a<0.

Hướng dẫn giải chi tiết:

a) Hàm số y = (m – 1)x + 3 là hàm số bậc nhất đối với x khi m – 1 ≠ 0 hay m ≠ 1 (*)

Hàm số đồng biến khi m – 1 > 0 hay m > 1.

Kết hợp với điều kiện (*) ta được với m > 1 thì hàm số đồng biến.

b) Hàm số y = (5 – k)x + 1 là hàm số bậc nhất đối với x khi 5 – k ≠ 0 hay k ≠ 5 (**).

Hàm số nghịch biến khi 5 – k < 0 hay k > 5.

Kết hợp với điều kiện (**) ta được với k > 5 thì hàm số nghịch biến.

Bài 33 (trang 61 SGK Toán 9 Tập 1): 

Với những giá trị nào của m thì đồ thị các hàm số y = 2x + (3 + m) và y = 3x + (5 – m) cắt nhau tại một điểm trên trục tung?

Phương pháp giải:

Hai đồ thị hàm số y=ax+b và y=a′x+b′ cắt nhau tại 1 điểm trên trục tung nếu {a≠a′ và b=b′}

Hướng dẫn giải chi tiết:

Đồ thị hai hàm số y = 2x + (3 + m) và y = 3x + (5 – m) cắt nhau tại một điểm trên trục tung nên ta thay hoành độ x = 0 vào:

    hàm số y = 2x + (3 + m) ta được tung độ: y = 3 + m

    hàm số y = 3x + (5 – m) ta được tung độ: y = 5 – m

Vì cùng là tung độ của giao điểm nên:

    3 + m = 5 – m => m = 1

Vậy khi m = 1 thì hai đường thẳng đã cho cắt nhau tại một điểm trên trục tung.

(Lưu ý: Điểm trên trục tung có hoành độ là 0)

Bài 34 (trang 61 SGK Toán 9 Tập 1): 

Tìm giá trị của a để hai đường thẳng y = (a – 1)x + 2 (a ≠ 1) và y = (3 – a)x + 1 (a ≠ 3) song song với nhau.

Phương pháp giải:

Hai đường thẳng  y=ax+b và y=a′x+b song song với nhau khi {a=a′ và b≠b′}

Hướng dẫn giải chi tiết:

Theo đề bài ta có b ≠ b' (vì 2 ≠ 1)

Nên hai đường thẳng y = (a – 1)x + 2 và y = (3 – a)x + 1 song song với nhau khi và chỉ khi:

    a – 1 = 3 – a

=> a = 2 (thỏa mãn a ≠ 1 và a ≠ 3)

Vậy với a = 2 thì hai đường thẳng song song với nhau.

Bài 35 (trang 61 SGK Toán 9 Tập 1): 

Xác định k và m để hai đường thẳng sau đây trùng nhau:

y = kx + (m – 2) (k ≠ 0);        

y = (5 – k)x + (4 – m) (k ≠ 5)

Phương pháp giải:

Hai đường thẳng y = ax + b (d) và y = a′x + b′ (d′), trong đó a và a' khác 0, ta có:

(d) và (d') trùng nhau khi và chỉ khi  a=a′, b=b′.

Hướng dẫn giải chi tiết:

Hai đường thẳng y = kx + (m – 2) và y = (5 – k)x + (4 – m) trùng nhau khi và chỉ khi:

    k = 5 – k (1) và m – 2 = 4 – m (2)

Từ (1) suy ra k = 2,5 (thỏa mãn điều kiện k ≠ 0 và k ≠ 5)

Từ (2) suy ra m = 3

Vậy với k = 2,5 và m = 3 thì hai đường thẳng trùng nhau.

►►Còn tiếp......

►Tải trọn bộ hướng dẫn giải bài tập toán Lớp 5 Ôn tập chương 2 - Hàm số bậc nhất tại đường link cuối bài.

Tổng hợp lý thuyết trọng tâm:

I. Chủ đề 1: Khái niệm hàm số

1. Khái niệm hàm số

• Nếu đại lượng y phụ thuộc vào đại lượng thay đổi x sao cho với mỗi giá trị của x, ta luôn xác định được chỉ một giá trị tương ứng của y thì y được gọi là hàm số của x, x được gọi là biến số.

• Hàm số có thể cho bằng bảng hoặc công thức.

• Khi x thay đổi mà y luôn nhận một giá trị không đổi thì hàm số y được gọi là hàm hằng.

2. Đồ thị hàm số

Đồ thị của hàm số y = f(x) là tập hợp tất cả các điểm biểu diễn các cặp giá trị tương ứng (x; f(x)) trên mặt phẳng tọa độ Oxy.

3. Hàm số đồng biến, nghịch biến.

Cho hàm số y = f(x) xác định trên tập số thực R Với x₁, x₂ ∈ R ta có:

• Nếu x₁ < x₂ mà f(x₁) < f(x₂) thì hàm số đồng biến.

• Nếu x₁ < x₂ mà f(x₁) > f(x₂) thì hàm số nghịch biến.

II. Chủ đề 2 - Hàm bậc nhất. Đồ thị hàm số: y = ax + b (a ≠ 0)

1. Định nghĩa

• Hàm số bậc nhất là hàm số được cho bởi công thức y = ax + b trong đó a, b là các số cho trước và a ≠ 0

• Đặc biệt, khi b = 0 thì hàm số bậc nhất trở thành hàm số y = ax , biểu thị tương quan tỉ lệ thuận giữa y và x.

2. Tính chất.

Hàm số bậc nhất y = ax + b xác định với mọi giá trị x ∈ R và có tính chất:

a) Đồng biến trên R, khi a > 0.

b) Nghịch biến trên R, khi a < 0.

3. Nhận xét về đồ thị hàm số y = ax + b (a ≠ 0) .

• Đồ thị hàm số y = ax (a ≠ 0) là một đường thẳng đi qua gốc tọa độ mà ta gọi là đường thẳng y = ax. Đường thẳng y = ax nằm ở góc phần tư thứ I và thứ III khi a > 0 ; nằm ở góc phần tư thứ II và thứ IV khi a < 0 .

• Đồ thị hàm số y = ax + b (a ≠ 0) là một đường thẳng:

• Cắt trục tung tại điểm có tung độ bằng b.

• Song song với đường thẳng y = ax nếu b ≠ 0 , và trùng với đường thẳng y = ax nếu b = 0

4. Cách vẽ đồ thị hàm số y = ax + b (a ≠ 0) .

• Bước 1: Cho x = 0 thì y = b , ta được điểm P(0; b) thuộc trục tung Oy.

Cho y = 0 thì x = -b/a ta được điểm Q(-b/a; 0) thuộc trục hoành

• Bước 2: Vẽ đường thẳng đi qua hai điểm P và Q ta được đồ thị hàm số y = ax + b (a ≠ 0) .

5. Kiến thức mở rộng

Trong mặt phẳng toạ độ, cho hai điểm A(x₁; y₂) ; B(x₂; y₂) ta có:

• 

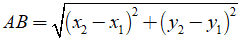
• M(x; y) là trung điểm của AB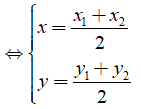 

• A đối xứng với B qua trục hoành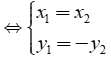 

• A đối xứng với B qua trục tung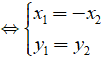 

• A đối xứng với B qua gốc O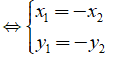 

• A đối xứng với B qua đường thẳng y = x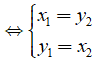 

• A đối xứng với B qua đường thẳng y = -x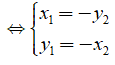 

III. Chủ đề 3: Đường thẳng song song và đường thẳng cắt nhau. Hệ số góc của đường thẳng y = ax + b (a # 0)

1. Đường thẳng song song, đường thẳng cắt nhau.

Cho hai đường thẳng (d₁ ): y = ax + b (a ≠ 0); (d₂): y = a'x + b' (a' ≠ 0)

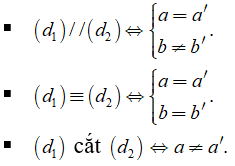
• Khi a ≠ 0 và b = b’ thì hai đường thẳng có cùng tung độ gốc, do đó chúng cắt nhau tại 1 điểm trên trục tung có tung độ là b.

2. Hệ số góc của đường thẳng y = ax + b (a ≠ 0)

* Cho đường thẳng y = ax + b (a ≠ 0) thì a được gọi là hệ số góc của đường thẳng.

* Tính chất

• Khi a > 0 thì góc tạo bởi đường thẳng y = ax + b và trục Ox là góc nhọn.Hệ số a càng lớn thì góc càng lớn nhưng vẫn nhỏ hơn 90°.

• Khi a < 0 thì góc tạo bởi đường thẳng y = ax + b và trục Ox là góc tù. Hệ số a càng lớn thì góc càng lớn nhưng vẫn nhỏ hơn 180°.

3. Kiến thức bổ sung

Cho hai đường thẳng (d₁): y = ax + b (a ≠ 0); (d₂): y = a'x + b' (a' ≠ 0) .

• (d₁) ⊥ (d₂) ⇔ a.a' = -1

• Nếu (d₁) cắt (d₂) thì hoành độ giao điểm là nghiệm của phương trình ax + b = a'x + b'

File tải hướng dẫn giải Bài: Ôn tập chương 2 Hàm số bậc nhất:

Hy vọng tài liệu sẽ hữu ích cho các em học sinh và quý thầy cô tham khảo và đối chiếu đáp án chính xác.

►Ngoài ra các em học sinh và thầy cô có thể tham khảo thêm nhiều tài liệu hữu ích hỗ trợ ôn luyện thi môn toán như đề kiểm tra, hướng dẫn giải sách giáo khoa, vở bài tập được cập nhật liên tục tại chuyên trang của chúng tôi.