Giải Toán lớp 9 trang 4, 5, 6, 7 SGK Tập 1 Bài 2: Căn bậc hai

Giải bài tập SGK Toán lớp 9 bài 1: Căn bậc hai được chúng tôi sưu tầm và đăng tải. Đây là lời giải kèm phương pháp giải hay các bài tập trong chương trình SGK Toán 9. Là tài liệu tham khảo hữu ích dành cho các em học sinh và quý thầy cô giáo tham khảo và đối chiếu đáp án chính xác, chuẩn bị tốt cho việc tiếp thu, giảng dạy bài học mới đạt hiệu quả.

Bài 1: Căn bậc hai

Trả lời câu hỏi Toán 9 Tập 1 Bài 1 trang 4:

Tìm các căn bậc hai của mỗi số sau:

a) 9;        b) 4/9;        c) 0,25;        d) 2.

Lời giải

a) Căn bậc hai của 9 là 3 và -3 (vì 3² = 9 và (-3)² = 9)

b) Căn bậc hai của 4/9 là 2/3 và (-2)/3 (vì (2/3)² = 4/9 và(-2/3)² = 4/9)

c) Căn bậc hai của 0,25 là 0,5 và -0,5 (vì 0,5² = 0,25 và (-0,5)² = 0,25)

d) Căn bậc hai của 2 là √2 và -√2 (vì (√2)² = 2 và(-√2)² = 2 ).

Trả lời câu hỏi Toán 9 Tập 1 Bài 1 trang 5: Tìm căn bậc hai số học của mỗi số sau:

a) 49;        b) 64;        c) 81;        d) 1,21.

Lời giải

a) √49 = 7, vì 7 > 0 và 7² = 49

b) √64 = 8, vì 8 > 0 và 8² = 64

c) √81 = 9, vì 9 > 0 và 9² = 81

d) √1,21 = 1,1 vì 1,1 > 0 và 1,1² = 1,21

Trả lời câu hỏi Toán 9 Tập 1 Bài 1 trang 5:

Tìm căn bậc hai của mỗi số sau:

a) 64;        b) 81;        c) 1,21.

Lời giải

a) Các căn bậc hai của 64 là 8 và -8

b) Các căn bậc hai của 81 là 9 và -9

c) Các căn bậc hai của 1,21 là 1,1 và -1,1

Trả lời câu hỏi Toán 9 Tập 1 Bài 1 trang 6: So sánh

a) 4 và √15;        b) √11 và 3.

Lời giải

a) 16 > 15 nên √16 > √15. Vậy 4 > √15

b) 11 > 9 nên √11 > √9. Vậy √11 > 3

Trả lời câu hỏi Toán 9 Tập 1 Bài 1 trang 6:

Tìm số x không âm, biết:

a) √x > 1;        b) √x < 3.

Lời giải

a) 1 = √1, nên √x > 1 có nghĩa là √x > √1

Vì x ≥ 0 nên √x > √1 ⇔ x > 1. Vậy x > 1

b) 3 = √9, nên √x < 3 có nghĩa là √x < √9

Vì x ≥ 0 nên √x < √9 ⇔ x < 9. Vậy x < 9

Bài 1 (trang 6 SGK Toán 9 Tập 1): 

Tìm căn bậc hai số học của mỗi số sau rồi suy ra căn bậc hai của chúng:

        121; 144; 169; 225; 256; 324; 361; 400

Lời giải:

Ta có: √121 = 11 vì 11 > 0 và 11² = 121 nên

Căn bậc hai số học của 121 là 11. Căn bậc hai của 121 là 11 và – 11.

Tương tự:

Căn bậc hai số học của 144 là 12. Căn bậc hai của 144 là 12 và -12.

Căn bậc hai số học của 169 là 13. Căn bậc hai của 169 là 13 và -13.

Căn bậc hai số học của 225 là 15. Căn bậc hai của 225 là 15 và -15.

Căn bậc hai số học của 256 là 16. Căn bậc hai của 256 là 16 và -16.

Căn bậc hai số học của 324 là 18. Căn bậc hai của 324 là 18 và -18.

Căn bậc hai số học của 361 là 19. Căn bậc hai của 361 là 19 và -19.

Căn bậc hai số học của 400 là 20. Căn bậc hai của 400 là 20 và -20.

Bài 2 (trang 6 SGK Toán 9 Tập 1): 

So sánh:

a) 2 và √3 ;     b) 6 và √41 ;     c) 7 và √47

Lời giải:

a) 2 = √4

Vì 4 > 3 nên √4 > √3 (định lí)

Vậy 2 > √3

b) 6 = √36

Vì 36 < 41 nên √36 < √41

Vậy 6 < √41

c) 7 = √49

Vì 49 > 47 nên √49 > √47

Vậy 7 > √47.

Bài 3 (trang 6 SGK Toán 9 Tập 1): 

Dùng máy tính bỏ túi, tính giá trị gần đúng của nghiệm mỗi phương tình sau (làm tròn đến chữ số thập phân thứ ba):

a) x² = 2 ;         b) x² = 3

c) x² = 3,5 ;         d) x² = 4,12

Hướng dẫn: Nghiệm của phương trình x² = a ( với a ≥ 0) là các căn bậc hai của a.

Lời giải:

a) x² = 2 => x₁ = √2 và x₂ = -√2

Dùng máy tính bỏ túi ta tính được:

    √2 ≈ 1,414213562

Kết quả làm tròn đến chữ số thập phân thứ ba là:

x₁ = 1,414; x₂ = - 1,414

b) x² = 3 => x₁ = √3 và x₂ = -√3

Dùng máy tính ta được:

    √3 ≈ 1,732050907

Vậy x₁ = 1,732; x₂ = - 1,732

c) x² = 3,5 => x₁ = √3,5 và x₂ = -√3,5

Dùng máy tính ta được:

    √3,5 ≈ 1,870828693

Vậy x₁ = 1,871; x₂ = - 1,871

d) x² = 4,12 => x₁ = √4,12 và x₂ = -√4,12

Dùng máy tính ta được:

    √4,12 ≈ 2,029778313

Vậy x₁ = 2,030 ; x₂ = - 2,030

Bài 4 (trang 7 SGK Toán 9 Tập 1): 

Tìm số x không âm, biết:

a) √x = 15;         b) 2√x = 14

c) √x < √2;         d) √2x < 4

Lời giải:

Lưu ý: Vì x không âm (x ≥ 0) nên các căn thức trong bài đều xác định.

a) √x = 15

Vì x ≥ 0 nên bình phương hai vế ta được:

x = 15² ⇔ x = 225

Vậy x = 225

b) 2√x = 14 ⇔ √x = 7

Vì x ≥ 0 nên bình phương hai vế ta được:

x = 7² ⇔ x = 49

Vậy x = 49

c) √x < √2

Vì x ≥ 0 nên bình phương hai vế ta được: x < 2

Vậy 0 ≤ x < 2

d)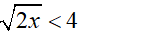 

Vì x ≥ 0 nên bình phương hai vế ta được:

2x < 16 ⇔ x < 8

Vậy 0 ≤ x < 8

Bài 5 (trang 7 SGK Toán 9 Tập 1): 

Đố. Tính cạnh một hình vuông, biết diện tích của nó bằng diện tích của hình chữ nhật có chiều rộng 3,5m và chiều dài 14m.

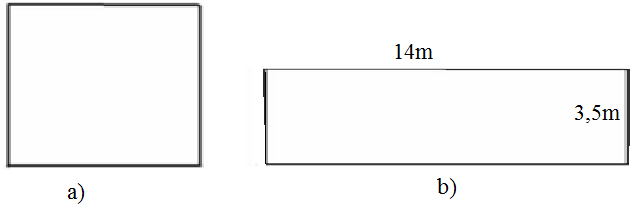
Hình 1

Lời giải:

Diện tích hình chữ nhật: S_HCN = 3,5.14 = 49 (m²)

Gọi a (m) (a > 0) là độ dài của cạnh hình vuông. Suy ra diện tích hình vuông là

S_HV = a² = 49 (m²)

=> a = 7 (m)

Vậy cạnh hình vuông có độ dài là 7m.

Ngoài ra các em học sinh và thầy cô có thể tham khảo thêm nhiều tài liệu hữu ích đầy đủ các môn được cập nhật liên tục tại chuyên trang của chúng tôi.

►►CLICK NGAY vào nút TẢI VỀ dưới đây để tải về hướng dẫn giải bài tập Toán lớp 9 SGK Tập 1 Bài 2: Căn bậc hai file Word, pdf hoàn toàn miễn phí!