Giải Toán lớp 9 trang 91, 92 SGK Tập 1 Bài: Ôn tập chương I

Giải bài tập sách giáo khoa Toán lớp 9 Bài: Ôn tập chương 1 trang 91, 92 được chúng tôi sưu tầm và đăng tải. Đây là lời giải kèm phương pháp giải hay các bài tập trong chương trình sách giáo khoa Toán 9. Là tài liệu tham khảo hữu ích dành cho các em học sinh và quý thầy cô giáo tham khảo và đối chiếu đáp án chính xác, chuẩn bị tốt cho việc tiếp thu, giảng dạy bài học mới đạt hiệu quả.

Ôn tập chương 1

Tổng hợp lý thuyết ôn tập chương 1

1. Hệ thức về cạnh và đường cao

Tam giác ABC vuông tại A, đường cao AH, ta có:

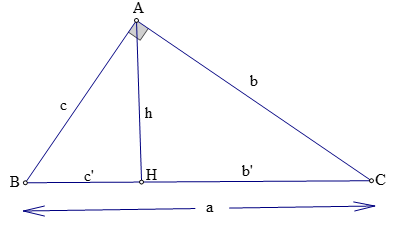
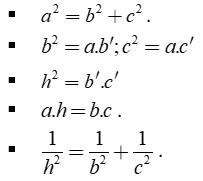
Chú ý: Diện tích tam giác vuông: S = (1/2)bc = (1/2)ah.

2. Tỉ số lượng giác của góc nhọn.

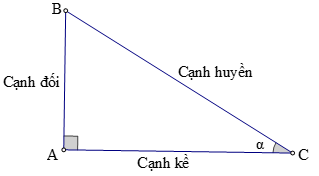
    + Tỉ số giữa cạnh đối và cạnh huyền được gọi là sin của góc α, kí hiệu là sinα.

    + Tỉ số giữa cạnh kề và cạnh huyền được gọi là côsin của góc α, kí hiệu là cosα.

    + Tỉ số giữa cạnh đối và cạnh kề được gọi là tang của góc α, kí hiệu là tanα.

    + Tỉ số giữa cạnh kề và cạnh đối được gọi là côtang của góc α, kí hiệu là cotα.

Hay sinα = AB/BC; cosα = AC/BC; tanα = AB/AC; cotα = AC/AB.

Tính chất:

    + Nếu α là một góc nhọn thì 0 < sinα < 1; 0 < cosα < 1; tanα > 0; cotα > 0.

    Ta có: sin²α + cos²α = 1;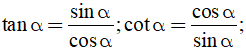 tanα.cotα = 1

    + Với hai góc nhọn α, β mà α + β = 90°.

    Ta có: sinα = cosβ; cosα = sinβ; tanα = cotβ; cotα = tanβ.

    Nếu hai góc nhọn α và β có sinα = sinβ hoặc cosα = cosβ thì α = β.

3. Hệ thức về cạnh và góc trong tam giác vuông.

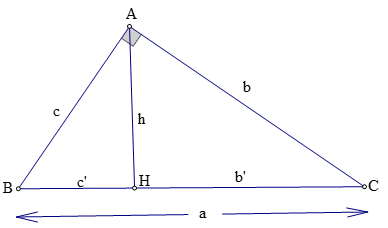
Trong một tam giác vuông, mỗi cạnh góc vuông bằng:

    + Cạnh huyền nhân với sin góc đối hay nhân với côsin góc kề.

    + Cạnh góc vuông kia nhân với tan của góc đối hay nhân với cotg của góc kề.

    b = a.sinB = a.cosC; c = a.sinC = a.cosB; b = c.tgB = c.cotgC; c = b.tgC = b.cotgC.

Chú ý: Trong một tam giác vuông nếu cho trước hai yếu tố (trong đó có ít nhất một yếu tố về cạnh và không kể góc vuông) thì ta sẽ tìm được các yếu tố còn lại.

Câu hỏi ôn tập chương 1

Câu 1 (trang 91 SGK Toán 9 Tập 1): 

Cho hình 36. Hãy viết hệ thức giữa:

a) Cạnh huyền, cạnh góc vuông và hình chiếu của nó trên cạnh huyền.

b) Các cạnh góc vuông p, r và đường cao h.

c) Đường cao h và hình chiếu của các cạnh góc vuông trên cạnh huyền p', r'

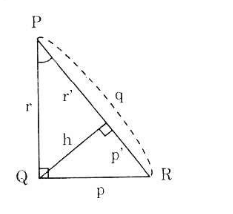
Hình 36

Trả lời:

a) p² = p'.q ; r² = r'.q

c) h² = p'.r'

Câu 2 (trang 91 SGK Toán 9 Tập 1): 

Cho hình 37.

a) Hãy viết công thức tính các tỉ số lượng giác của góc α

b) Hãy viết hệ thức giữa các tỉ số lượng giác của góc α và các tỉ số lượng giác của góc β.

Trả lời:

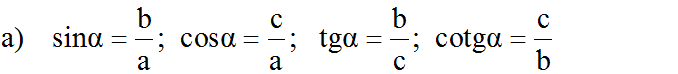
b) sin α = cos β;         cos α = sin β

tg α = cotg β;         cotg α = tgβ

Câu 3 (trang 91-92 SGK Toán 9 Tập 1): 

Xem hình 37.

a) Hãy viết công thức tính các cạnh góc vuông b và c theo cạnh huyền a và tỉ số lượng giác của các góc α, β.

b) Hãy viết công thức tính mỗi cạnh góc vuông theo cạnh góc vuông kia và tỉ số lượng giác của các góc α, β.

Trả lời:

a) b = asin α = acosβ; c = asinβ = acosα

b) b = c.tanα = c.cotβ

c = b.tanβ = b.cotα

Câu 4 (trang 92 SGK Toán 9 Tập 1): 

Để giải một tam giác vuông, cần biết ít nhất mấy góc và cạnh? Có lưu ý gì về số cạnh?

Trả lời:

Để giải một tam giác vuông cần biết hai yếu tố trong đó có ít nhất là một yếu tố cạnh.

Ngoài ra các em học sinh và thầy cô có thể tham khảo thêm nhiều tài liệu hữu ích đầy đủ các môn được cập nhật liên tục tại chuyên trang của chúng tôi.

►►CLICK NGAY vào nút TẢI VỀ dưới đây để tải về Giải Toán lớp 9 SGK Tập 1 trang 91, 92 Bài: Ôn tập chương I file Word, pdf hoàn toàn miễn phí!