Giải Toán lớp 9 trang 71, 72 SGK Tập 2: Liên hệ giữa cung và dây cung

Giải bài tập SGK Toán lớp 9 bài 2: Liên hệ giữa cung và dây cung được chúng tôi sưu tầm và đăng tải. Đây là lời giải kèm phương pháp giải hay các bài tập trong chương trình SGK Toán 9. Là tài liệu tham khảo hữu ích dành cho các em học sinh và quý thầy cô giáo tham khảo và đối chiếu đáp án chính xác, chuẩn bị tốt cho việc tiếp thu, giảng dạy bài học mới đạt hiệu quả.

Giải toán lớp 9 SGK Tập 2 trang 71, 72

Trả lời câu hỏi Toán 9 Tập 2 Bài 2 trang 71:

Hãy chứng minh định lý trên.

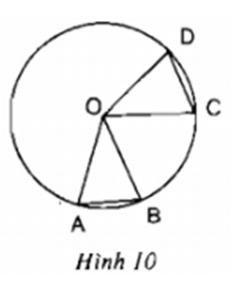
Lời giải

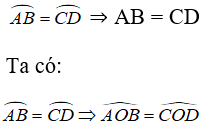
Xét ΔOAB và ΔOCD có:

OA = OC = R

góc AOB = góc COD

OB = OD = R

⇒ ΔOAB = ΔOCD (c.g.c)

⇒ AB = CD ( hai cạnh tương ứng)

b) AB = CD ⇒ cung AB = cung CD

Xét ΔOAB và ΔOCD có:

OA = OC = R

AB = CD (gt)

OB = OD = R

⇒ ΔOAB = ΔOCD (c.c.c)

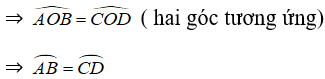
Trả lời câu hỏi Toán 9 Tập 2 Bài 2 trang 71:

Xem hình 11.

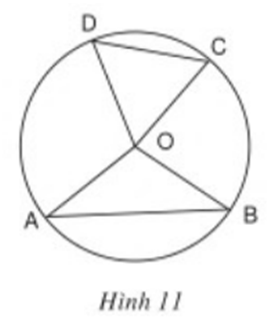
Hãy viết giả thiết và kết luận của định lý

(Không yêu cầu học sinh chứng minh định lý này)

Lời giải

Cung AB > cung CD => AB > CD

AB > CD => Cung AB > cung CD

Bài 10 (trang 71 SGK Toán 9 Tập 2):

a) Vẽ đường tròn tâm O, bán kính R = 2cm. Nêu cách vẽ cung AB có số đo bằng 60^o. Hỏi dây AB dài bao nhiêu xentimet?

b) Làm thế nào để chia được đường tròn thành sáu cung bằng nhau như trên hình 12?

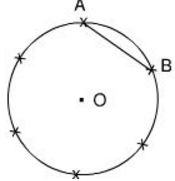
Hình 12

Lời giải

a) + Dùng compa vẽ đường tròn tâm O, bán kính R = 2cm.

+ Trên đường tròn lấy điểm A.Nối OA từ đó vẽ góc AOB = 60^o

Khi đó ta được cung AB có số đo bằng 60º.

+ ΔAOB có OA = OB, góc AOB = 60^o

⇒ ΔAOB đều

⇒ AB = OA = OB = R = 2cm.

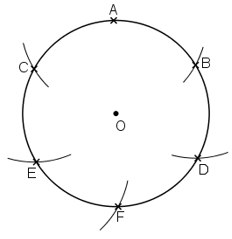
b) Chia đường tròn thành 6 cung bằng nhau:

+ Vẽ đường tròn tâm O, bán kính R.

+ Trên đường tròn tâm O, lấy điểm A.

+ Vẽ cung tròn tâm A, bán kính R cắt đường tròn tại B và C.

+ Vẽ cung tròn tâm B và C bán kính R cắt đường tròn tâm O tại giao điểm thứ hai là D và E.

+ Vẽ cung tròn tâm E bán kính R cắt đường tròn (O) tại giao điểm thứ hai là F.

Khi đó, ta chia được đường tròn thành sáu cung bằng nhau như trên

Bài 11 (trang 72 SGK Toán 9 tập 2):

Cho hai đường tròn bằng nhau (O) và (O') cắt nhau tại hai điểm A và B. Kẻ các đường kính AOC, AO'D. Gọi E là giao điểm thứ hai của AC với đường tròn (O').

a) So sánh các cung nhỏ BC, BD.

b) Chứng mình rằng B là điểm chính giữa của cung EBD (tức là điểm B chia cung EBD thành hai cung bằng nhau: cung BE = cung BD).

Phương pháp giải:

+ Với hai cung nhỏ trong cùng một đường tròn hoặc hai đường tròn bằng nhau thì hai dây bằng nhau căng hai cung bằng nhau.

Lời giải

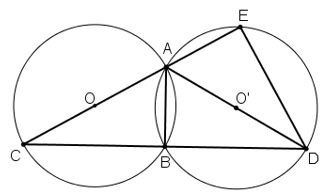
a) Vì A,B,C ∈ (O)

⇒ BO = OA = OC

⇒ BO = AC/2.

Tam giác ABC có đường trung tuyến BO và BO bằng một phần hai độ dài cạnh tương ứng AC

=> Tam giác ABC là tam giác vuông tại B ( định lí)

⇒ góc ABC = 90^o

Chứng minh tương tự

=> Góc ABD = 90^o

Đường tròn tâm O và O’ bằng nhau ⇒ AC = AD.(AC,AD lần lượt là bán kính của (O) và (O’))

Xét hai tam giác vuông ΔABC và ΔABD có:

AB chung, AC = AD

⇒ ΔABC = ΔABD (cạnh huyền – cạnh góc vuông)

⇒ BC = BD(hai cạnh tương ứng)

⇒ cung BC = cung BD ( định lý )

b) Xét tam giác AED có đường trung tuyến EO' bằng một phần hai cạnh tương ứng là AD ( O'E = O'A = O'D = AD/2)

=> Tam giác AED vuông tại E

⇒ Góc AED = 90^o hay góc CED = 90^o

⇒ ΔECD vuông tại E.

Ta có:

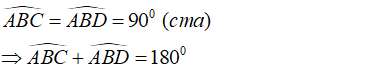
Suy ra: C, B, D thẳng hàng.

Tam giác ECD vuông có EB là đường trung tuyến ứng với cạnh huyền( Vì BC = BD câu (a) )

⇒ EB = BD (CD/2).

⇒ Cung BE = cung BD (định lý) hay B là điểm chính giữa cung EBD.

Bài 12 (trang 72 SGK Toán 9 Tập 2):

Cho tam giác ABC . Trên tia đối của tia AB lấy một điểm D sao cho AD = AC. Vẽ đường tròn tâm O ngoại tiếp tam giác DBC. Từ O lần lượt hạ các đường vuông góc OH, OK với BC và BD (H ∈ BC, K ∈ BD)

a) Chứng minh rằng OH > OK.

b) So sánh hai cung nhỏ BD và BC.

Phương pháp giải:

+ Trong một đường tròn, dây nào lớn hơn thì dây đó gần tâm hơn

+ Trong một đường tròn, dây lớn hơn căng cung lớn hơn.

Lời giải

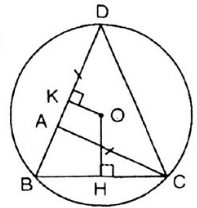
a) Xét ΔABC có: BC < AB + AC (Bất đẳng thức tam giác)

Mà AD = AC (gt)

⇒ BC < AB + AD = BD

Mà OH là khoảng cách từ O đến dây BC

OK là khoảng cách từ O đến dây BD

⇒ OH > OK.( định lý về khoảng cách từ tâm đến dây)

b) Vì BD > BC

⇒ cung BD > cung BC.

Bài 13 (trang 72 SGK Toán 9 Tập 2):

Chứng minh rằng: trong một đường tròn, hai cung bị chắn giữa hai dây song song thì bằng nhau.

Phương pháp giải:

+ Trong một đường tròn, hai dây bằng nhau căng hai cung bằng nhau.

+ Trong cùng một đường tròn, hai cung được gọi là bằng nhau nếu chúng có số đo bằng nhau, tức là góc ở tâm chắn hai cung đó bằng nhau.

Lời giải

Vẽ đường tròn tâm O, các dây cung AB // CD.

Cần chứng minh cung AC = cung BD.

Cách 1:

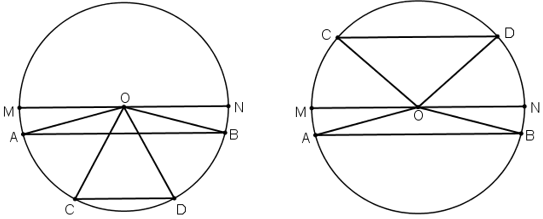
Kẻ bán kính MN // AB // CD

MN // AB

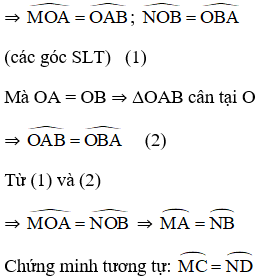
+ TH1: AB và CD cùng nằm trong một nửa đường tròn.

.

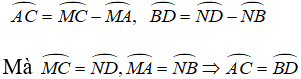+ TH2: AB và CD thuộc hai nửa đường tròn khác nhau.

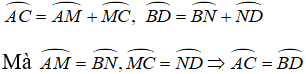
Bài 14 (trang 72 SGK Toán 9 Tập 2):

a) Chứng minh rằng đường kính đi qua điểm chính giữa của một cung thì đi qua trung điểm của dây cung căng cung ấy. Mệnh đề đảo có đúng không? Hãy nêu thêm điều kiện để mệnh đề đảo đúng.

b) Chứng minh rằng đường kính đi qua điểm chính giữa của một cung thì vuông góc với dây cung ấy và ngược lại.

Lời giải

a)

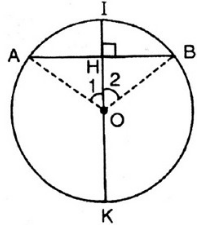
Vẽ đường tròn tâm O, dây cung AB.

Gọi I là điểm chính giữa của cung AB.

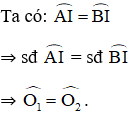
Gọi OI ∩ AB = H.

ΔAOH và ΔBOH có: AO = OB, Góc O₁ = Góc O₂ ; OH chung

⇒ ΔAOH = ΔBOH (c-g-c)

⇒ AH = BH (hai cạnh tương ứng)

⇒ OI đi qua trung điểm H của AB.

+ Mệnh đề đảo: Đường kính đi qua trung điểm của một dây cung thì đi qua điểm chính giữa của cung đó.

Mệnh đề sai

Ví dụ: Chọn dây cung AB là một đường kính của (O) (AB đi qua O). Khi đó, tồn tại đường kính CD đi qua O là trung điểm của AB nhưng C,D không phải là điểm chính giữa cung AB ( hình vẽ)

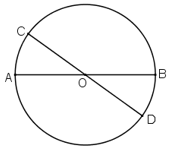
Mệnh đề đảo chỉ đúng khi dây cung AB không phải đường kính.

b)

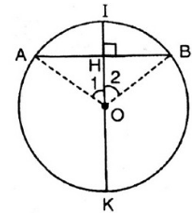
+ Cho đường tròn (O); dây cung AB ;

I là điểm chính giữa cung AB, H = OI ∩ AB.

⇒ ΔAOH = ΔBOH (cm phần a).

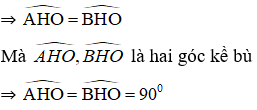
⇒ OH ⊥ AB.

Vậy đường kính đi qua điểm chính giữa của cung thì vuông góc với dây căng cung ấy.

+ Cho đường tròn (O); dây cung AB.

Kẻ đường thẳng OH ⊥ AB (H ∈ AB) cắt đường tròn tại I.

Ta có: ΔABO cân tại O (vì AO = OB = R).

⇒ đường cao OH đồng thời là đường phân giác

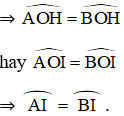
⇒ I là điểm chính giữa của cung AB

Vậy đường kính vuông góc với dây căng cung thì đi qua điểm chính giữa của cung.

Ngoài ra các em học sinh và thầy cô có thể tham khảo thêm nhiều tài liệu hữu ích đầy đủ các môn được cập nhật liên tục tại chuyên trang của chúng tôi.

►►CLICK NGAY vào nút TẢI VỀ dưới đây để tải về hướng dẫn giải bài tập Toán lớp 9 SGK Tập 2 trang 71, 72 file Word, pdf hoàn toàn miễn phí!