Giải Toán lớp 9 trang 5, 7 SGK Tập 2 (Chính xác nhất)
Giải bài tập SGK Toán lớp 9 bài 1: Phương trình bậc nhất hai ẩn được chúng tôi sưu tầm và đăng tải. Đây là lời giải kèm phương pháp giải hay các bài tập trong chương trình SGK Toán 9. Là tài liệu tham khảo hữu ích dành cho các em học sinh và quý thầy cô giáo tham khảo và đối chiếu đáp án chính xác, chuẩn bị tốt cho việc tiếp thu, giảng dạy bài học mới đạt hiệu quả
Giải Toán 9 SGK Tập 2 Bài 1: Phương trình bậc nhất hai ẩn
Giải Toán lớp 9 SGK Tập 2 trang 5, 7
Trả lời câu hỏi Toán 9 Tập 2 Bài 1 trang 5 (1):
a) Kiểm tra xem các cặp số (1; 1) và (0,5; 0) có là nghiệm của phương trình 2x – y = 1 hay không ?
b) Tìm thêm một nghiệm khác của phương trình 2x – y = 1.
Lời giải
a) Cặp số (1; 1) là nghiệm của phương trình 2x – y = 1 vì 2.1 – 1 = 1
Cặp số (0,5; 0) là nghiệm của phương trình 2x – y = 1 vì 2.0,5 – 0 = 1
b) Chọn x = 2 ta có: 2.2 – y = 1 ⇔ y = 3
Vậy cặp số (2; 3) là một nghiệm của phương trình 2x – y = 1
Trả lời câu hỏi Toán 9 Tập 2 Bài 1 trang 5 (2):
Nêu nhận xét về số nghiệm của phương trình 2x – y = 1.
Lời giải
Chọn x = x0 ( x0 ∈ R) ta có : 2x0 - y = 1 ⇔ y = 2x0 -1
Suy ra , mọi cặp số dạng (x0; 2x0 -1 )với x0 tùy ý đều là nghiệm của phương trình 2x - y = 1
Phương trình 2x – y = 1 có vô số nghiệm
Trả lời câu hỏi Toán 9 Tập 2 Bài 1 trang 5 (3):
Điền vào bảng sau và viết ra sáu nghiệm của phương trình (2):
| x | -1 | 0 | 0,5 | 1 | 2 | 2,5 |
| y = 2x – 1 |
Lời giải
| x | -1 | 0 | 0,5 | 1 | 2 | 2,5 |
| y = 2x – 1 | -3 | -1 | 0 | 1 | 3 | 4 |
Vậy 6 nghiệm của phương trình là : (-1; -3), (0; -1), (0,5; 0), (1; 1), (2; 3), (2,5; 4)
Bài 1 (trang 7 SGK Toán 9 Tập 2):
Trong các cặp số (-2; 1), (0; 2), (-1; 0), (1, 5; 3) và (4; -3) cặp số nào là nghiệm của phương trình:
a) 5x + 4y = 8? ;
b) 3x + 5y = -3?
Phương pháp giải:
Cặp số (x0; y0) là nghiệm của phương trình ax + by = c ⇔ ax0 + by0 = c.
Lời giải
a) Xét cặp (-2; 1). Thay x = -2 ; y = 1 vào phương trình 5x + 4y = 8 ta được :
5x + 4y = 5.(-2) + 4.1 = -10 + 4 = -6 ≠ 8
⇒ cặp số (-2; 1) không là nghiệm của phương trình 5x + 4y = 8.
Xét cặp(0; 2). Thay x = 0 ; y = 2 vào phương trình 5x + 4y = 8 ta được
5x + 4y = 5.0 + 4.2 = 8
⇒ cặp số (0; 2) là nghiệm của phương trình 5x + 4y = 8.
Xét cặp (-1; 0). Thay x = -1 ; y = 0 vào phương trình 5x - 4y = 8 ta được:
5x + 4y = 5.(-1) + 4.0 = -5 ≠ 8
⇒ cặp số (-1; 0) không là nghiệm của phương trình 5x + 4y = 8.
Xét cặp (1,5 ; 3). Thay x = 1,5 ; y = 3 vào phương trình 5x + 4y = 8 ta được
5x + 4y = 5.1,5 + 4.3 = 7,5 + 12 = 19,5 ≠ 8
⇒ (1,5; 3) không là nghiệm của phương trình 5x + 4y = 8.
Xét cặp (4;-3).Thay x = 4 ; y = -3 vào phương tình 5x + 4y = 8 ta được:
5x + 4y = 5.4 + 4.(-3) = 20 – 12 = 8
⇒ (4; -3) là nghiệm của phương trình 5x + 4y = 8.
Vậy có hai cặp số (0; 2) và (4; -3) là nghiệm của phương trình 5x + 4y = 8.
b) Xét cặp số (-2; 1).Thay x = -2 ; y = 1 vào phương trình 3x + 5y = -3 ta được:
3x + 5y = 3.(-2) + 5.1 = -6 + 5 = -1 ≠ -3
⇒ (-2; 1) không là nghiệm của phương trình 3x + 5y = -3.
Xét cặp số (0; 2) . Thay x = 0 ; y = 2 vào phương trình 3x + 5y = -3 ta được:
3x + 5y = 3.0 + 5.2 = 10 ≠ -3
⇒ (0; 2) không là nghiệm của phương trình 3x + 5y = -3.
Xét cặp (-1; 0).Thay x = -1 ; y = 0 vào phương trình 3x + 5y = -3 ta được:
3x + 5y = 3.(-1) + 5.0 = -3
⇒ (-1; 0) là nghiệm của phương trình 3x + 5y = -3. .
Xét cặp (1,5; 3). Thay x = 1,5 ; y = 3 vào phương trình 3x + 5y = -3 ta được:
3x + 5y = 3.1,5 + 5.3 = 4,5 + 15 = 19,5 ≠ -3
⇒ (1,5; 3) không là nghiệm của phương trình 3x + 5y = -3.
Xét cặp (4; -3). Thay x = 4 ; y = -3 vào phương trình 3x + 5y = -3 ta được:
3x + 5y = 3.4 + 5.(-3) = 12 – 15 = -3
⇒(4; -3) là nghiệm của phương trình 3x + 5y = -3.
Vậy có hai cặp số (-1; 0) và (4; -3) là nghiệm của phương trình 3x + 5y = -3.
Bài 2 (trang 7 SGK Toán 9 Tập 2):
Với mỗi phương trình sau, tìm nghiệm tổng quát của phương trình và vẽ đường thẳng biểu diễn tập nghiệm của nó:
a) 3x – y = 2;
b) x + 5y = 3;
c) 4x – 3y = -1;
d) x + 5y = 0 ;
e) 4x + 0y = -2 ;
f) 0x + 2y = 5.
Lời giải
a) 3x – y = 2 (1)
⇔ y = 3x – 2.
Vậy phương trình có nghiệm tổng quát là (x; 3x – 2) (x ∈ R).
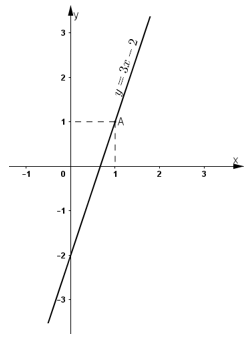
Đường thẳng biểu diễn tập nghiệm của phương trình (1) là đường thẳng y = 3x – 2 (Hình vẽ).
+ Tại x = 2/3 thì y = 0 ⇒ đường thẳng y = 3x – 2 đi qua điểm (2/3 ; 0).
+ Tại x = 0 thì y = -2 ⇒ đường thẳng y = 3x – 2 đi qua điểm (0; -2).
Vậy đường thẳng y = 3x – 2 là đường thẳng đi qua điểm (2/3 ; 0) và (0; -2).
b) x + 5y = 3 (2)
⇔ x = 3 – 5y
Vậy phương trình có nghiệm tổng quát là (3 – 5y; y) (y ∈ R).
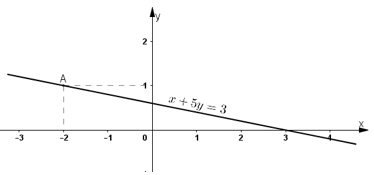
Đường thẳng biểu diễn tập nghiệm của (2) là đường thẳng x + 5y = 3.
+ Tại y = 0 thì x = 3 ⇒ Đường thẳng đi qua điểm (3; 0).
+ Tại x = 0 thì y = 3/5 ⇒ Đường thẳng đi qua điểm (0; 3/5).
Vậy đường thẳng x + 5y = 3 là đường thẳng đi qua hai điểm (3; 0) và (0; 3/5).
c) 4x – 3y = -1
⇔ 3y = 4x + 1
⇔ y = 4/3x + 1/3
Vậy phương trình có nghiệm tổng quát là (x; 4/3x + 1/3) (x ∈ R).
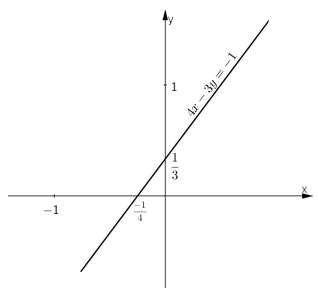
Đường thẳng biểu diễn tập nghiệm phương trình là đường thẳng 4x – 3y = -1.
+ Tại x = 0 thì y = 1/3
Đường thẳng đi qua điểm (0; 1/3)
+ Tại y = 0 thì x = -1/4
Đường thẳng đi qua điểm (-1/4; 0)
Vậy đường thẳng 4x – 3y = -1 đi qua (0; 1/3) và (-1/4; 0)
d) x + 5y = 0
⇔ x = -5y.
Vậy nghiệm tổng quát của phương trình là (-5y; y) (y ∈ R).
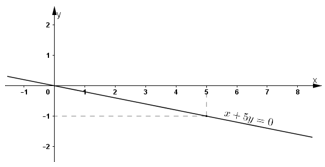
Đường thẳng biểu diễn nghiệm của phương trình là đường thẳng x + 5y = 0.
+ Tại x = 0 thì y = 0 ⇒ Đường thẳng đi qua gốc tọa độ.
+ Tại x = 5 thì y = -1 ⇒ Đường thẳng đi qua điểm (5; -1).
Vậy đường thẳng x + 5y = 0 đi qua gốc tọa độ và điểm (5; -1).
e) 4x + 0y = -2
⇔ 4x = -2 ⇔ x = -1/2
Phương trình có nghiệm tổng quát (-0,5; y)(y ∈ R).
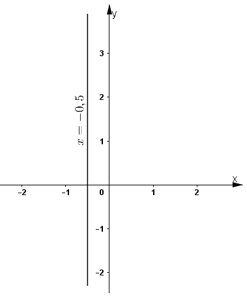
Đường thẳng biểu diễn tập nghiệm là đường thẳng x = -0,5 đi qua điểm (-0,5; 0) và song song với trục tung.
f) 0x + 2y = 5
<=> 2y = 5 <=> y = 5/2
Phương trình có nghiệm tổng quát (x; 2,5) (x ∈ R).
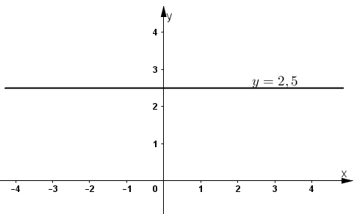
Đường thẳng biểu diễn tập nghiệm là đường thẳng y = 2,5 đi qua điểm (0; 2,5) và song song với trục hoành.
Bài 3 (trang 7 SGK Toán 9 Tập 2):
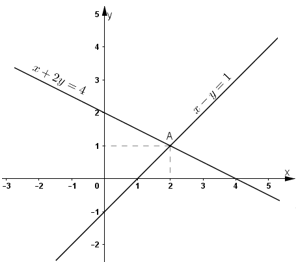
Cho hai phương trình x + 2y = 4 và x – y = 1. Vẽ hai đường thẳng biểu diễn tập nghiệm của hai phương trình đó trên cùng một hệ tọa độ. Xác định tọa độ giao điểm của hai đường thẳng và cho biết tọa độ của nó là nghiệm của các phương trình nào.
Lời giải
- Vẽ đường thẳng x + 2y = 4.
+ Với x = 0 ⇒ y = 2. Đường thẳng đi qua điểm (0; 2).
+ Với y = 0 ⇒ x = 4. Đường thẳng đi qua điểm (4; 0).
Đường x + 2y = 4 là đường thẳng đi qua điểm (0; 2) và (4; 0).
- Vẽ đường thẳng x – y = 1
+ Với x = 0 ⇒ y = -1. Đường thẳng đi qua điểm (0; -1).
+ Với y = 0 ⇒ x = 1. Đường thẳng đi qua điểm (1; 0).
Đường x – y = 1 là đường thẳng đi qua điểm (0 ; -1) và (1 ; 0).
- Giao điểm của hai đường thẳng là điểm A có tọa độ là (2; 1).
- Ta có A(2; 1) cùng thuộc hai đường thẳng nên nó là nghiệm của cả hai phương trình đã cho.
Ngoài ra các em học sinh và thầy cô có thể tham khảo thêm nhiều tài liệu hữu ích đầy đủ các môn được cập nhật liên tục tại chuyên trang của chúng tôi.
►►CLICK NGAY vào nút TẢI VỀ dưới đây để tải về hướng dẫn giải bài tập Toán lớp 9 SGK Tập 2 trang 5, 7 file Word, pdf hoàn toàn miễn phí!
- Chọn lọc 77 Bài Toán giải phương trình bậc 2 chứa tham số m
- Giải bài toán bằng cách lập hệ phương trình lớp 9 trang 23, 24 (Tập 2)
- Giải Toán 9 Bài 4: Giải hệ phương trình bằng phương pháp cộng đại số
- Giải Toán lớp 9 trang 44, 45 SGK Tập 2 (Chính xác nhất)
- Giải Bài 3: Giải hệ phương trình bằng phương pháp thế Toán 9
- Giải Toán lớp 9 trang 49, 50 Bài: Luyện tập SGK Tập 2
- Giải Toán lớp 9 trang 34 - 39 SGK Tập 2: Bài Đồ thị hàm số y = ax2 (a ≠0)
- Giải Toán lớp 9 trang 8, 9, 10, 11, 12 SGK Tập 2 (Chính xác nhất)