Giải Toán lớp 9 trang 73, 75, 76 SGK Tập 2 Bài 3: Góc nội tiếp

Giải bài tập SGK Toán lớp 9 bài 3: Góc nội tiếp được chúng tôi sưu tầm và đăng tải. Đây là lời giải kèm phương pháp giải hay các bài tập trong chương trình SGK Toán 9. Là tài liệu tham khảo hữu ích dành cho các em học sinh và quý thầy cô giáo tham khảo và đối chiếu đáp án chính xác, chuẩn bị tốt cho việc tiếp thu, giảng dạy bài học mới đạt hiệu quả.

Giải Toán lớp 9 SGK Tập 2 trang 73, 75, 76

Giải bài tập Toán lớp 9 SGK Tập 2 Bài 3: Góc nội tiếp trang 73, 75

Trả lời câu hỏi Toán 9 Tập 2 Bài 3 trang 73 (1):

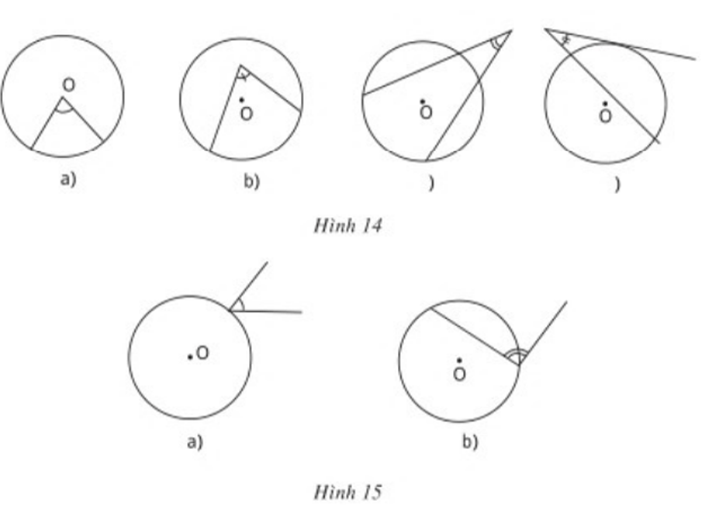
Vì sao các góc ở hình 14 và hình 15 không phải là góc nội tiếp ?

Lời giải

Các góc trên hình 14 không phải góc nội tiếp vì các góc này không có đỉnh nằm trên đường tròn

Các góc trên hình 15 không phải góc nội tiếp vì các góc này không có hai cạnh chứa hai dây cung của đường tròn.

Trả lời câu hỏi Toán 9 Tập 2 Bài 3 trang 73 (2):

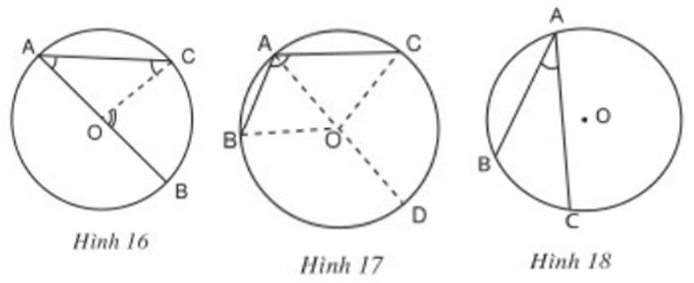
Bằng dụng cụ, hãy so sánh số đo của góc nội tiếp ∠(BAC) với số đo của cung bị chắn BC trong mỗi hình 16, 17, 18 dưới đây.

Lời giải

Sử dụng thước đo độ để đo các góc, từ đó ta rút ra kết luận:

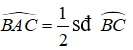
Trả lời câu hỏi Toán 9 Tập 2 Bài 3 trang 75 (3):

Hãy vẽ hình minh họa các tính chất trên.

Lời giải

a) Các góc nội tiếp bằng nhau chắn các cung bằng nhau

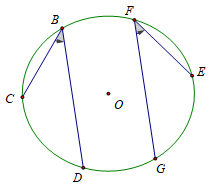
b) Các góc nội tiếp cùng chắn một cung hoặc chắn các cung bằng nhau thì bằng nhau

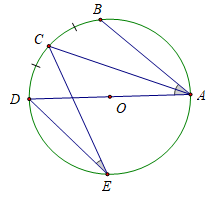
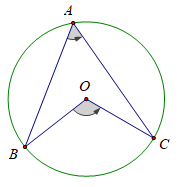
c) Góc nội tiếp (nhỏ hơn hoặc bằng 90^o) có số đo bằng nửa số đo góc ở tâm cùng chắn một cung

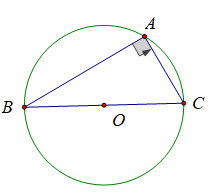
d) Góc nội tiếp chắn nửa đường tròn là góc vuông

Bài 15 (trang 75 SGK Toán 9 Tập 2):

Các khẳng định sau đây đúng hay sai?

a) Trong một đường tròn, các góc nội tiếp cùng chắn một cung thì bằng nhau.

b) Trong một đường tròn, các góc nội tiếp bằng nhau thì cùng chắn một cung.

Phương pháp giải:

Định lý: Trong một đường tròn, số đo của góc nội tiếp bằng nửa số đo của cung bị chắn.

Hệ quả: Trong một đường tròn, các góc nội tiếp bằng nhau chắn các cung bằng nhau.

Lời giải

a) Đúng (theo hệ quả b).

b) Sai. Vì trong cùng một đường tròn, các góc nội tiếp cùng chắn 1 cung hoặc chắn các cung bằng nhau thì bằng nhau.

Trong một đường tròn, các góc nội tiếp bằng nhau chưa chắc cùng chắn một cung.

Bài 16 (trang 75 SGK Toán 9 Tập 2):

Xem hình 19 (hai đường tròn có tâm là B, C và điểm B nằm trên đường tròn tâm C).

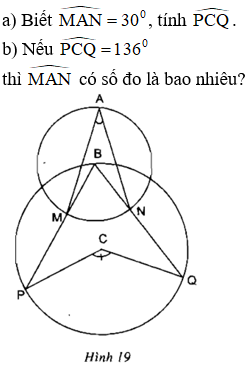
Phương pháp giải:

Trong một đường tròn, góc nội tiếp có số đo bằng nửa số đo của góc ở tâm cùng chắn một cung.

Lời giải

a) Đường tròn tâm B có góc MAN là góc nội tiếp chắn cung MN; Góc MBN là góc ở tâm chắn cung MN

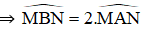
Đường tròn tâm C có Góc MBN là góc nội tiếp chắn cung PQ; góc PCQ là góc ở tâm chắn cung PQ.

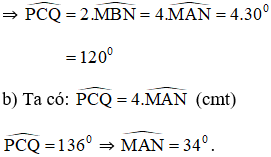
Bài 17 (trang 75 SGK Toán 9 Tập 2):

Muốn xác định tâm của một đường tròn mà chỉ dùng êke thì phải làm như thế nào?

Lời giải

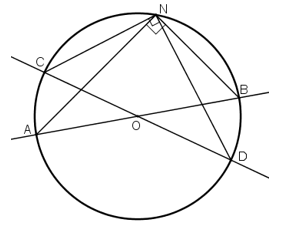
Áp dụng hệ quả: Góc nội tiếp chắn nửa đường tròn là góc vuông.

Cách xác định:

+ Đặt đỉnh vuông của eke trùng với một điểm N bất kỳ trên đường tròn, kẻ đường thẳng đi qua cạnh huyền của êke cắt đường tròn tại A và B ta được đường kính AB.

+ Vẫn đặt đỉnh vuông của eke tại N, xoay eke theo hướng khác, kẻ đường thẳng đi qua cạnh huyền của êke cắt đường tròn tại C và D ta được đường kính CD.

+ CD cắt AB tại tâm O của đường tròn.

Bài 18 (trang 75 SGK Toán 9 Tập 2):

Một huấn luyện viên cho cầu thủ tập sút bóng vào cầu môn PQ. Bóng được đặt ở các vị trí A, B, C trên một cung tròn như hình 20.

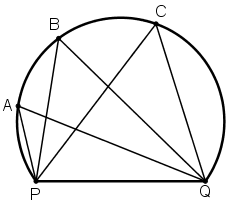
Hãy so sánh các góc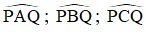 

Phương pháp giải:

+ Trong cùng một đường tròn, các góc nội tiếp cùng chắn một cung thì bằng nhau.

Lời giải

Các điểm A, B, C, Q, P cùng thuộc một đường tròn.

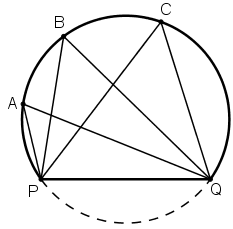
Các góc PAQ; PBQ; PCQ đều là các góc nội tiếp cùng chắn cung PQ.

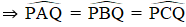
Giải bài tập Toán lớp 9 SGK Tập 2 Luyện tập Bài 3: Góc nội tiếp trang 75, 76

Bài 19 (trang 75 SGK Toán 9 Tập 2):

Cho đường tròn tâm O, đường kính AB và S là một điểm nằm bên ngoài đường tròn. SA và SB lần lượt cắt đường tròn tại M, N. Gọi H là giao điểm của BM và AN. Chứng minh rằng SH vuông góc với AB.

Phương pháp giải:

+ Góc nội tiếp chắn nửa đường tròn là góc vuông.

+ Trong một tam giác, ba đường cao đồng quy tại trực tâm.

Lời giải

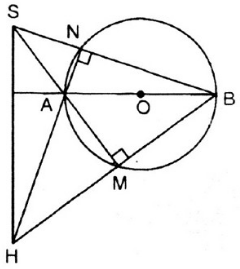
Góc ANB là góc nội tiếp chắn nửa đường tròn ⇒ Góc ANB = 90^o ⇒ AN ⊥ NB

Góc AMB là góc nội tiếp chắn nửa đường tròn ⇒ Góc AMB = 90^o ⇒ AM ⊥ MB

ΔSHB có: SM ⊥ HB, NH ⊥ SB và SM; HN cắt nhau tại A.

⇒ A là trực tâm của ΔSHB.

⇒ AB ⊥ SH (đpcm).

Bài 20 (trang 76 SGK Toán 9 Tập 2):

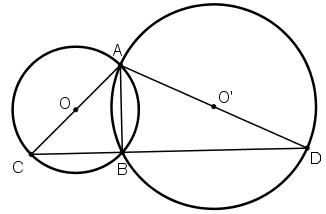
Cho hai đường tròn (O) và (O') cắt nhau tại A và B. Vẽ các đường kính AC và AD của hai đường tròn. Chứng minh rằng ba điểm C, B, D thẳng hàng.

Phương pháp giải:

+ Trong một đường tròn, góc nội tiếp chắn nửa đường tròn là góc vuông.

Lời giải

Trong đường tròn tâm O, Góc ABC là góc nội tiếp chắn nửa đường tròn

=> Góc ABC = 90^o

Trong đường tròn tâm O’, Góc ABD là góc nội tiếp chắn nửa đường tròn

Suy ra, ba điểm C, B và D thẳng hàng.

Bài 21 (trang 76 SGK Toán 9 Tập 2):

Cho hai đường tròn bằng nhau (O) và (O') cắt nhau tại A và B. Vẽ đường thẳng qua A cắt (O) tại M và cắt (O') tại N (A nằm giữa M và N). Hỏi MBN là tam giác gì? Tại sao?

Phương pháp giải:

+ Trong cùng một đường tròn hoặc hai đường tròn bằng nhau, hai dây bằng nhau căng hai cung bằng nhau.

+ Trong một đường tròn, số đo của góc nội tiếp bằng nửa số đo của cung bị chắn.

Lời giải

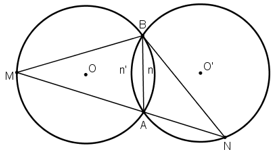
+ (O) và (O’) là hai đường tròn bằng nhau

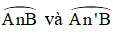 cùng được căng bởi dây AB

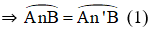
+ (O) có góc BMA là góc nội tiếp chắn cung AnB

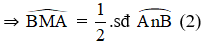
+ (O’) có góc BNA là góc nội tiếp chắn cung An'B

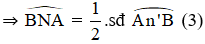
Từ (1); (2); và (3) suy ra góc BMA = góc BNA

⇒ ΔBMN cân tại B.

Bài 22 (trang 76 SGK Toán 9 Tập 2):

Trên đường tròn (O) đường kính AB, lấy điểm M (khác A và B). Vẽ tiếp tuyến của (O) tại A. Đường thẳng BM cắt tiếp tuyến đó tại C. Chứng minh rằng ta luôn có:

MA² = MB . MC

Lời giải

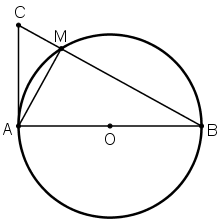
Góc AMB là góc nội tiếp chắn nửa đường tròn

=> Góc AMB = 90^o

AC là tiếp tuyến của đường tròn tại A

⇒ AC ⊥ AO

=> Góc CAB = 90^o

⇒ ΔABC vuông tại A có đường cao AM

⇒ AM² = MB.MC (Hệ thức về cạnh và đường cao trong tam giác vuông).

Bài 23 (trang 76 SGK Toán 9 Tập 2):

Cho đường tròn (O) và một điểm M cố định không nằm trên đường tròn. Qua M kẻ hai đường thẳng . Đường thẳng thứ nhất cắt (O) tại A và B. Đường thẳng thứ hai cắt (O) tại C và D. Chứng minh MA.MB = MC.MD.

Hướng dẫn: Xét cả hai trường hợp điểm M nằm bên trong và bên ngoài đường tròn. Trong mỗi trường hợp, xét hai tam giác đồng dạng.

Phương pháp giải:

+ Góc nội tiếp chắn một cung có số đo bằng một nửa số đo của cung đó.

+ Hai góc nội tiếp chắn cùng một cung thì có số đo bằng nhau.

Lời giải

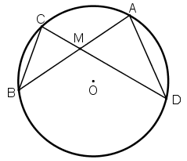
TH1: M nằm trong đường tròn.

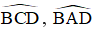 là hai góc nội tiếp cùng chắn cung BD

⇒ MA.MB = MC.MD

TH2: M nằm ngoài đường tròn.

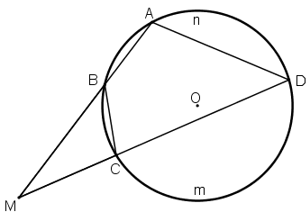
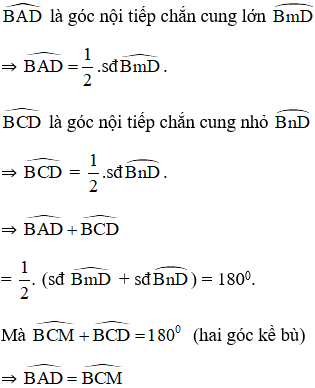
ΔMBC và ΔMDA có:

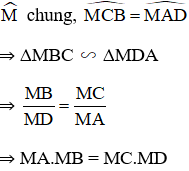
Bài 24 (trang 76 SGK Toán 9 Tập 2):

Một chiếc cầu được thiết kế như hình 21 có độ dài AB = 40m, chiều cao MK = 3m. Hãy tính bán kính của đường tròn chứa cung AMB.

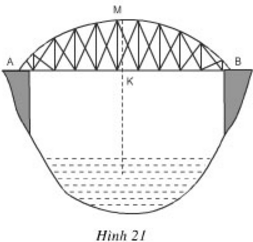
Lời giải

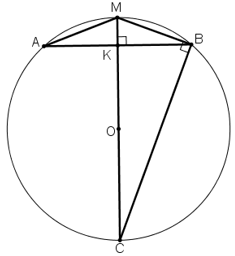
Gọi (O; R) là đường tròn chứa cung AMB.

Kẻ đường kính MC.

K là trung điểm AB ⇒ BK = AB/2 = 20 (m).

Góc MBC là góc nội tiếp chắn nửa đường tròn

⇒ Góc MBC = 90º

⇒ ΔMBC vuông tại B, có BK là đường cao

⇒ BK² = MK.KC ( hệ thức về cạnh và đường cao trong tam giác vuông)

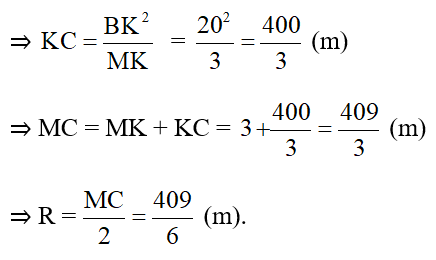
Bài 25 (trang 76 SGK Toán 9 Tập 2):

Dựng một tam giác vuông, biết cạnh huyền dài 4cm và một cạnh góc vuông dài 2,5cm.

Phương pháp giải:

Góc nội tiếp chắn một nửa đường tròn là góc vuông.

Lời giải

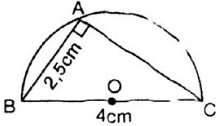
Cách vẽ như sau:

- Vẽ đoạn thẳng BC dài 4cm.

- Vẽ nửa đường tròn đường kính BC.

- Vẽ đường tròn tâm B bán kính 2,5cm cắt nửa đường tròn đường kính BC tại A.

Ta có tam giác thỏa mãn các yêu cầu của đề bài.

Bài 26 (trang 76 SGK Toán 9 Tập 2):

Cho AB, BC, CA là ba dây của đường tròn (O). Từ điểm chính giữa M của cung AB vẽ dây MN song song với dây BC.Gọi giao điểm của MN và AC là S.Chứng minh SM = SC và SN = SA.

Phương pháp giải:

Trong một đường tròn:

+ Số đo của góc nội tiếp bằng một nửa số đo của cung bị chắn.

+ Hai cung bị chắn giữa hai dây song song thì bằng nhau.

Lời giải

 

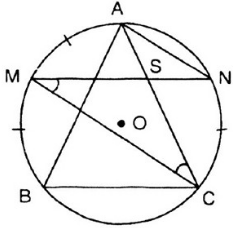
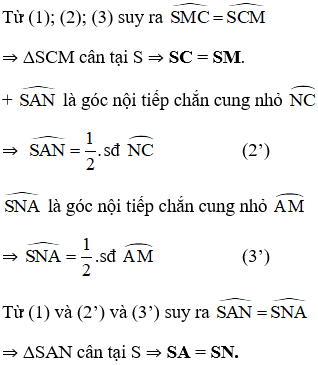
Ngoài ra các em học sinh và thầy cô có thể tham khảo thêm nhiều tài liệu hữu ích đầy đủ các môn được cập nhật liên tục tại chuyên trang của chúng tôi.

►►CLICK NGAY vào nút TẢI VỀ dưới đây để tải về hướng dẫn giải bài tập Toán lớp 9 SGK Tập 2 Bài 3: Góc nội tiếp file Word, pdf hoàn toàn miễn phí!